| 【授業研究３】 高等学校数学Ⅱ 「三角関数」 | |||||
| ア | 授業の構想 | ||||
本研究主題に迫るための授業を構想するにあたり，授業実践クラスで授業に関する意識調査を行った。この調査結果では，「自分の考え方と友達の考え方を比べて違いが分かったとき」の回答数に着目した。授業中に発表する機会や互いの考えを述べ合うことは，小学校，中学校，高等学校と校種が進むにつれて減ってくる傾向があると思われる。特に，高等学校では，講義形式の授業が多くなり，友達の考えを聞き，自分と比較しながら，様々なことを考え，吸収するということが減ってきているのではないかと思われる。質問２の「熱中したり満足したりする授業」では，生徒は「一人で考える時間が十分にある授業」「やグループで活動したり，友達と話し合ったりする授業」の回答数が多くなっている。これは，じっくり考え込んでみたい，友達から様々な意見を聞きたいという願いがあるものと考えられる。実際に，テストの採点をしているとき，生徒の解答に今後の学習内容に踏み込んでいるものや，考え方のさらなる発展性，有用性が見込めるもの意外性のある解法等，様々な発想がうかがえ教師が高く評価したくなることがある。そのような解答にこそ，生徒個々の考え方の違いがあるように思え，興味深い。その見方，考え方の違いを授業の中で認め合い，比較し，吸収し合うことで新しい知識等や考え方を得ることができ，さらにそれぞれの見方や考え方， を高めることは「学ぶ楽しさや充実感」を味わうことにつながるととらえ，指導法の工夫を考えることとした。 |
|||||
| イ | 指導の手だて | ||||
| (ア) | 多様な考え方を引き出す学習課題について | ||||
| 生徒それぞれがもつ考え方をより多く引き出すために，まず正答に至る考え方が多岐にわたる問題を生徒に解かせ，生徒の解法のすべてを学習課題にしようと考えた。正答誤答を問わず，生徒の解答をタイプ別に集計し，生徒の解答を一覧できるプリントを作成し，それを学習課題提示の場面で活用する授業を構成し，それぞれの生徒の考え方を生かした授業を展開する。 | |||||
| (イ) | 生徒一人一人がじっくり考え，自分なりの解決を図ることについて | ||||
| まず，前時に，本時の学習課題にかかわる問題を生徒に解かせる。次時の学習の予告を兼ねるとともに，その際，より多様で独創的な生徒の解法を期待し，解決に十分な時間をかける。また，自分なりの解決の見通しや解答に至る過程を記入させ，次時の授業に用いるようにする。 | |||||
| (ウ) | 多様な考え方を生かすことについて | ||||
| 正答，誤答，それぞれの「考え方」について吟味したり，練り上げたりする授業を展開する。特に誤答に目を向け，誤答となった要因を探ったり，その解法の改善点を指摘したり，誤答から得られた結果をさらに深く考えるなど，今後の発展性が見込めるものについては，具体的に提示したり紹介したりしながら，生徒が考えを巡らせるような授業を行う。 | |||||
| (エ) | 教具の工夫について | ||||
| 本時において「グラフの値の和」を視覚的にとらえやすくするために，ｙの値を表す板磁石を利用する。これは，本時の授業における発展した考え方を示したり，考えを深めたりする際に活用する。 | |||||
| ウ | 授業の展開 | ||||
| (ア) | 目標 | ||||
| 三角関数の合成について，生徒一人一人がじっくり考え，様々な考え方に基づき，多方面から課題に取り組み，学習内容の理解を深める。また，発展性のある考え方を学び，今後の学習に役立てようとする。 | |||||
| (イ) | 準備 | ||||
| 教科書，解法を整理したプリント，グラフの和の理解補助のためのマグネット（板磁石） | |||||
| (ウ) | 学習指導案 | ||||
 |
|||||
| エ | 授業の記録 | ||||
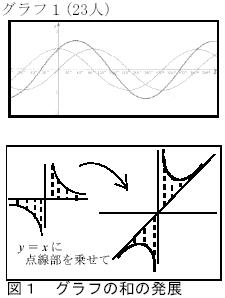グラフ１からグラフ８は，生徒が前時に問題を解いたものである。回答数とそれぞれの生徒の考え方をプリントにし，学習課題として提示した。なお，括弧の中には生徒数を記す。正答であるグラフ１での考え方，授業での指導内容は以下のとおりであった。(複数回答を含む。) ① 代表的なθを代入，計算し，予想をたてかいた（12人） ②のア 値の和に注目しグラフをかいた（10人） ②のイ sin θのグラフに各θのcos θの値を乗せた（２人） ③ 曲線と曲線の和は曲線になると思った（１人） グラフは代表的な値を計算し，点を座標平面に置き直線や曲線で結ぶという考え方でかいたものが多った。その考え方が一番わかりやすいのであるが，後の授業で解説した，ｙ＝(－２)x 等は整数値xで代表点をとるとグラフをかけないことがあり，代表点を結ぶ時にはグラフを表す式や意味等にもっと注意しなければならない。②のイの考え方を話題に取り上げ，その考えを発展させるものとして，ｙ＝ｘ＋１／ｘのグラフを紹介した。数学Ⅲで出てくるこのグラフは，微分，増減，極限による漸近線を求める作業でかくことが基本であるが，ｙ＝ｘの値を基本とし，板磁石を使い任意のの値に対するの値を表す線分を載せてみると，現段階でも簡単にかくことができる（図１参照）。このグラフは，どうなるという疑問の問いかけに，かいてみようとする生徒が多数いた。また，③の考え方については，特別な状況で直線になる以外は曲線であること，さらにフーリエ級数についてもごく簡単にではあるが紹介してみた。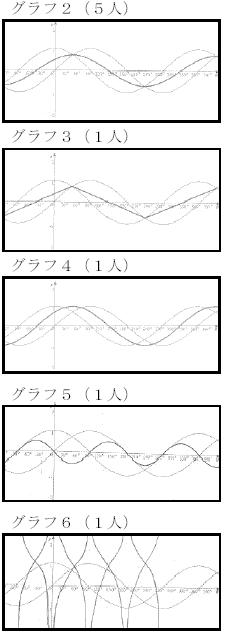 
グラフ２，３，４は「真ん中を通る」という考え方のもとにイメージでかいたものである。「真ん中を通る」という解釈は二つである。あるθにおけるｙの値の中間，またはｙ＝ sin θから見た，ｙ＝ cos θへの移動の中間という解釈ができる｡（グラフ２，４） 代表値を計算し，点を平面上に置き，結ぶという作業で容易に起こりうる誤答がグラフ３である。（代表点が少ない両グラフの交点を通りそうという予想のみ）中で直線で結びたくなったのだと思う。正弦曲線で結ばれるということは合成一般形を用い，式の上で確認することが大事であると指導した。これらの誤答からはグラフ２においては平均ととらえることができるのでｙ＝（sin θ＋cos θ）÷２と表すことができること，またグラフ３では正弦から見た余弦の平行移量90°の確認，およびｙ＝ sin（θ＋45°）を確認した。どちらのグラフも生徒の気持ちは手に取るように分かるというのが率直な感想である。同じ感想を抱いた生徒が多くいた。 グラフ５が描かれた背景には計算の理解不足があった。 ｙ＝ sin θ＋sin(90°＋θ）＝ sin（2θ＋90°） ＝ sin2(θ＋45°） アンダーライン部がそれである。この計算について，不具合なことは，角度の和を計算したことであり，三角関数の性質ではこのような式変形がないことを確認した。 グラフ６は下のような計算を行ったが，左辺分母cos θの処理に困ってしまい，場合分けをイメージして±１としたようである。ｙをθの関数として表すことを指導した。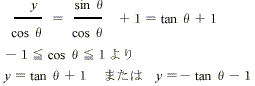 
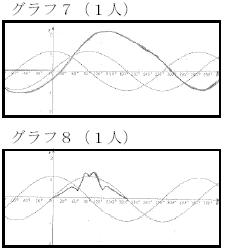グラフ７は自然現象をイメージしたのだろうか，波と波が相乗効果で津波のように大きくなると考えている。正弦曲線の波が大きくなる関数としてはｙ＝ｘ sin ｘ（ただしｘ：rad）が数学Ⅲで紹介されているので触れてみた。ただ，弧度法の説明から始めなければならず，簡単に説明したものの，理解した生徒は少なかったと思われる。しかし，発展的に考えていく関数のグラフに興味をもつ生徒もいた。グラフ８は勘違いから代表値をかけ算して点を求めてしまったようである。 また，グラフがかけなかった生徒が１名いたが，代表値を求めて，試行錯誤しながらかこうとしていた。 |
|||||
| オ | 授業の考察 | ||||
| (ア) | 授業についての実態調査 | ||||
今回の授業実践後，授業についての実態調査を実施した。この結果を見ると，生徒は十分に「楽しさ」を感じるまでには至らなかった。「いつもの授業より深く考えることができた」，「様々な考えを知ることは有意義だった」と答えた生徒はクラスの半数程おり，「充実感」ということにおいては成果が上がったと考えられる。生徒からの感想でも，「様々な角度からアプローチすることで深く掘り下げることができた」，「他のクラスの解答も見てみたい」，「発展的な内容でこの形態をとるとよい」等といった感想があった。一方では，理解力のある生徒からは，「解き方や考え方をすぐに教わった方がよい」，「時間がかかりすぎる」といった感想もあった。友達などの多様な見方，考え方に触れ，自分なりの解決を図ることには興味をもっているので，授業を行うに際しては今後の授業進度に遅れがないよう，時間数の確保に努めなければならないと思った。 |
|||||
| (イ) | 学習課題について | ||||
| 今回の学習課題では８種類グラフの解答を提示することができた。このように多くの解答が得られた理由として，生徒の考える時間を十分に取ったことがあげられる。１問をじっくり考えさせたことで各生徒が自分の考え方を構築でき，自分なりに解くことができたものと考える。学習課題とする問題も難易度が適切であり，適度な正解数を得られたことにより，課題に対する生徒の積極的な意欲を喚起できたと考える。また，誤答についての学習では，間違いを起こしやすいグラフのイメージや計算の部分を確認することができ，発展としての内容も数学Ⅲにまで踏み込んだものなども，この授業で触れることができた。学習課題の設定がうまくいったことが，生徒の学ぶことへの充実感につながったと考える。 | |||||
| (ウ) | 教具について | ||||
| 正弦，余弦グラフの代表的な点について和を求める際，板磁石を利用したことは，「理解に役だった」と話してくれた生徒もいたように有効であったと思われる。さらに，生徒はより視覚的に式の意味をとらえることができ，その重要性に気付いたようである。簡単な教具ではあるものの，工夫することでその教材の理解の手助けとなり，発展的な内容を考える際にも効果的であった。今後，複雑に構成された式に直面したときにも，本時で学習したことが生かされてくると考える。 | |||||
| カ | 授業研究のまとめ | ||||
| 今回実施した授業方法は，「生徒自らが学習課題をつくり，解決していく学習」という見方もできると思う。生徒が主体となって，自らが課題を創り出し，その課題に積極的に取り組み，解決することにより，生徒は新しい知識等を素直に受け入れられたと思う。 グラフの和と三角関数の合成の一般形を一斉授業で行った後，本授業を実践したが，１単位時間をかけて，じっくりとプリントの内容を考えるような時間の余裕が欲しかった。生徒に解かせる問題の選定や生徒が十分に考える時間のさらなる確保を，今後の課題としたい。 |
|||||