| 【授業研究２】 中学校第１学年 課題学習「ガウス少年に挑戦」 | |||||||||||||||||||
| ア | 授業の構想 | ||||||||||||||||||
本研究主題に迫るためには，生徒が，日々の数学の授業で楽しいと感じるときはどんなときかをとらえ，授業を構成する必要があると考え，数学の授業で楽しいと感じるときについての意識調査（表１）を実施した。この調査結果から，問題の内容や意味が分かり，解決の見通しをもって，試行錯誤しながら問題が解決できたときや，解決の過程で新たな方法や考え方に気付いたり，見いだしたり，知識を再構成できたときに楽しさを味わうという生徒の姿がうかがえる｡このことを踏まえ，数学史から，有名な「ガウスの計算」を学習の素材として扱い，第１学年において課題学習を設定した。 本単元の学習では，生徒が図形的に見る見方や式を工夫して処理する考え方などのよさを実感し，さらに，それらの数学的な見方や考え方を活用して，課題を発展できるようにしたい。 なお，本単元を設定するにあたっては，以下の三点に視点を置き，単元構成の工夫をし，この学習活動を通して，生徒は数学を学ぶ楽しさや充実感を味わえると考える。
|
|||||||||||||||||||
| イ | 指導の手だて | ||||||||||||||||||
| (ア) | 課題設定の工夫 | ||||||||||||||||||
既習の内容から見方や考え方を深めさせたいと考え，以下に示す小学校第４学年で学習している課題を利用した。
この課題は，数量関係の内容であるが，事前に「下の図のように，正方形を１段，２段，３段，…と並べていきます。このとき，あなたは，どのような問題を作りますか。」という実態調査（平成14年９月13日実施 中学校第１学年34人）を行った。 その結果，約９割の生徒が，○番目の正方形の数を求める問題を作った。そこで，生徒全員が問題の意味が分かり，自分の問題として意欲的に取り組めるように，本時では○番目の正方形の数を求める課題を設定することとした。 |
|||||||||||||||||||
| (イ) | 数学的な見方や考え方のよさを実感し，課題を発展的に考察できる単元構成の工夫 | ||||||||||||||||||
| 中学校の数学の学習では，小学校で身に付けてきた基礎的な知識や技能をもとに，さらに数学的に見る見方や考える力を高めることが大切であると考える。 例えば，小学校で学習している（□＋○）×△＝□×△＋○×△を２つの長方形の面積の和として見る見方を生かし，第１学年の文字式で５ｘ＋２ｘ＝７ｘを導く考え方や第３学年の多項式で正方形から長方形に変形して，それらの面積の関係から（ｘ＋ａ)(ｘ－ａ）＝ｘ²－ａ²を導く考え方などである。 そこで，本単元では，数学的な見方や考え方のよさを再認識し，それらを活用していけるように以下のような指導計画（２時間扱い）で授業を実施した。  第１時では，規則的に並べた正方形の数を数える活動からその規則性を式に表せること，式に表せることによって形式的に処理できること，また，式で処理する操作が，図形でも同じように考えられることを考察させたい。 第２時は，新たに得た数学的な見方や考えを発展的に活用できるように，第１時で学習したことをもとに問題作りを行い，その問題を解決する学習活動である。 |
|||||||||||||||||||
| (ウ) | 生徒の多様な見方や考え方に応じるための支援の工夫 | ||||||||||||||||||
| 生徒が解決する方法は，図をかいて正方形の数を数えようとする方法，式をたてて計算で処理しようとする方法，さらには，前の図形の個数から関数的に考えようとする方法など，多種多様であることが予想される。また，図で考えた生徒の中に，例えば，10番目の場合に，10＋９＋…２＋１を10＋(10－１)＋(10－２)…＋(10－８)＋(10－９)と見る生徒もいると思われる。 このように，生徒一人一人の多様な考え方を把握するとともに，つまずいている生徒に対して的確な支援ができるようにティーム・ティーチングによる指導形態を取り入れる。さらに，より効果的に援助・指導ができるように座席表を利用した補助簿を活用し，教師間で相互に生徒の取り組み具合の実態を確認しながら授業を進めるようにする。 |
|||||||||||||||||||
| ウ | 授業の展開 | ||||||||||||||||||
 |
|||||||||||||||||||
| エ | 授業の記録 | ||||||||||||||||||
生徒の考え方を記録した座席表と授業での観察から，第１時の授業の様子を以下に示す。 第２時では，ほとんどの生徒が，グループになって友達と相談しながら問題作りを行っていた。生徒たちが作った問題は，以下の図１のとおりである。 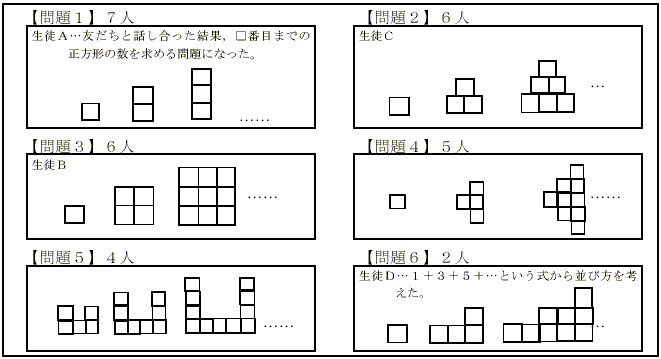 図１ 生徒が作った問題（例） |
|||||||||||||||||||
| オ | 授業の考察 | ||||||||||||||||||
| 生徒が充実感を味わえるようにするためには，まず生徒全員が，「できること」や「分かること」を実感することが大切であると考える。授業実践後，解決方法は異なるが，全員が結果を導け，単元構成の工夫が生かされたと思われる。また，学ぶ楽しさを実感できたかどうかについては，図２の調査１から生徒全員が課題を解決し，その解決の方法について考えることができ，「楽しかった」と感じている生徒が多かったと思われる。調査２のオとカの人数が多いことは，比較・検討の場で，自分の解決方法とは違う多様な見方や考え方のよさに触れることによって，「考えた」という楽しさを生徒自身が実感できたからであると考えられる。 しかし，「第２時でとても楽しかった」という生徒が減少したことについては，問題作りをした経験がないという生徒が多く，どのように問題を作ってよいのか，どう発展させていったらよいのかが，分からなかったためではないかと考える。 さらに，下の資料２の生徒の感想にある「驚いた」，「すごい」，「うれしい」などから，式を工夫して処理する考え方のよさや図形的に見る見方のよさなどに触れ，数学的に考える楽しさを実感できたと考える。また，問題作りの活動でも，「また，作りたい」等の生徒の声が聞かれ，生徒の活動の充実ぶりがうかがえた。
|
|||||||||||||||||||
| カ | 授業研究のまとめ | ||||||||||||||||||
| 本単元の学習を通して，数学的な見方や考え方のよさに触れることによって，今まで以上に数学を学ぶ楽しさや充実感を味わわせることができた。しかし，数名の生徒から，「授業が早く進んだので，もっとゆっくり考えたかった」，「自分なりに納得するまでに，時間がかかった」という感想も見られた。生徒の多様な見方や考え方に応じるという点からは，一人一人の生徒の願いや考えを把握する必要があった。 数学を学ぶ楽しさは，生徒自らが，試行錯誤したり創意工夫したりしながら，数学的な見方や考え方を味わい，そしてその見方や考え方を発展させたり，活用させたりという数学的活動から得られるものと思う。生徒が考えようとしている意欲と，どのように考えているかという視点を的確に教師が把握できるように，今後は，評価の工夫が必要であると考える。 |
|||||||||||||||||||
