| �@�y���ƌ����R�z | |||||||||||||||||||||||||||||||||||||||||||||
| �@ | �@�����w�Z1�N����̏���� | ||||||||||||||||||||||||||||||||||||||||||||
| �@ | (1) | �@���Ƃ̍\�z | |||||||||||||||||||||||||||||||||||||||||||
| �@ | 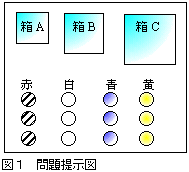 �@���{�̐��w����̎���Ƃ��āC�w�͒����ł̓g�b�v�N���X�ł���̂ɑ��āC���k�̈ӎ��̏�ł͐��w�������Ɗ����鐶�k�̊������������Ă���B�l�����錴���Ƃ��ẮC���t���������ނ悤�ȍu�`�`���̎��Ƃ������s���Ă��邱�ƁC���w�������̒��łǂ̂悤�ɖ𗧂��Ă���̂����Ȃ��Ȃ������o���Ȃ����ƁC�]���̎d������Ɏ����ɂ����@�ł��邱�ƂȂǂ���������B �@���{�̐��w����̎���Ƃ��āC�w�͒����ł̓g�b�v�N���X�ł���̂ɑ��āC���k�̈ӎ��̏�ł͐��w�������Ɗ����鐶�k�̊������������Ă���B�l�����錴���Ƃ��ẮC���t���������ނ悤�ȍu�`�`���̎��Ƃ������s���Ă��邱�ƁC���w�������̒��łǂ̂悤�ɖ𗧂��Ă���̂����Ȃ��Ȃ������o���Ȃ����ƁC�]���̎d������Ɏ����ɂ����@�ł��邱�ƂȂǂ���������B�@���̔��ȂƂ��ċ��߂�ꂽ���̂��C�V�w�K�w���v�̂̉��P�̂˂炢�ł�����C�{�����̃e�[�}�ł����颎���w�ю���l����͂��琬����w�K�w���v�⢐��w�I�����̊y�����𖡂키�w�K�w����ł���ƍl������B�����,���k�������Ŏ����������������肷�邱�Ƃ�, ����ɑ��̐��k�Ƃ̃R�~���j�P�[�V������ʂ��āC���炪���w���w�K���邱�Ƃ̂悳�𗝉����C���w�I�����̊y�����𖡂킢�C��̓I�w�K�ւƕω����Ă������Ƃ����߂��Ă���̂��Ǝv����B �@�����ŁC�{�����ł͐��k�����ۂɎ����ł��C�����k�ɂƂ��Đg�߂ȑ�ނƂ��āu���̏�����Ƃ����P�������グ�邱�Ƃɂ������̓I�ɂ�,��`�C�a�C�b�̂R�̔��ƐԁC���C�C���̋ʂ��R������B���܁C�R�̔��ɋʂ��P�������B�������C�ԋʂ͏��Ȃ��Ƃ��P�͓������̂Ƃ���B���̂Ƃ��C�R�̔��͋�ʂ�����̂Ƃ��C���F�̋ʂ͋�ʂ��Ȃ����̂Ƃ���ƁC���ʂ�̓���������邩���Ƃ������ł���B���̖��͉��ʂ���̉��������o������ł���B�{���Ƃł́C���t�̑�����͖��̈Ӗ��̊m�F�Ƃ��̉�@�̗���̊m�F������݂̂ŁC��͑S�ʓI�ɐ��k�̎���I�Ȋ����ɔC���邱�Ƃɂ����B�܂��C����������ł̓���(�F���M�C���͂���)����p�ӂ��C���̎g�p���@�ɂ��ẮC���k�����ɍD���Ȃ悤�ɗ��p�������B����ɁC�̏������ɂ��āC�����炩��w�����邱�ƂȂ����R�ɋL�q�������B�����āC�X�̉�@�̊��z�ɂ��Ă����ꂼ��̐��k�̎��_���珑�����邱�Ƃɂ����B�܂�C���t�̃C���[�W�����^�ɓ��Ă͂߂�̂łȂ��C���k�̌X�̐��w�̔\�͂⊈���o���̈Ⴂ���l�����Ή������邱�Ƃɂ��C���k�̎�̓I�Ȑ��w�̊w�K���o���C����ɂ���l��l�̐��k�����w�I�����̊y�����𖡂킢�C����Ɏ���w�ю���l����w�K�ւƕϊ����鑫������ɂȂ�Ƃ������҂������Ď��Ƃ̍\�z���s�����B |
||||||||||||||||||||||||||||||||||||||||||||
| (2) | �@�w���̎肾�� | ||||||||||||||||||||||||||||||||||||||||||||
| �@ | �A | �@���ɂ��� | |||||||||||||||||||||||||||||||||||||||||||
| �@ | �@ | �@�O���Ɍ������Ǝ��Ɋw�K�������z��C���̈� ���̊m�F���s�����B�܂��C�ǂ̂悤�ȍl����������� �����邩�Ƃ����A�C�f�A���e���ǒ��ɕ��Ă����� ���Ɏw�����Ă������B���̒i�K�ł́C�O���[�v�S�̂� �b�����̂ł͂Ȃ��C�����܂ł��l�ŃA�C�f�A���l�� ��������̂ł���B���̓J���[�v�����g�������̂� �S���ɔz�z���C���ł����l�̃��f����p�ӂ����B | |||||||||||||||||||||||||||||||||||||||||||
| �@ | �C | �@��@�̊m�F�ƃq���g�̃v�����g�ɂ��� | |||||||||||||||||||||||||||||||||||||||||||
| �@ | �@ |  �@�l�������@�Ƃ��āC�X�p�ӂ��Ă������B���̂����̂T��(��@1����5�܂�)�͑S���̃O���[�v�����g�݁C�]�T������Ή�@�U����X�ɂ����g�܂���B��̓I�ɂ́C���őS�̂ɐ���������,��@�P����T�܂ł̃q���g�̎�(�v�_���܂Ƃ߂�����)�Ɖp����z������ȉ��ɁC��@�P����X�y�уq���g�Ƃ��Ĕz�z�����\�������B �@�l�������@�Ƃ��āC�X�p�ӂ��Ă������B���̂����̂T��(��@1����5�܂�)�͑S���̃O���[�v�����g�݁C�]�T������Ή�@�U����X�ɂ����g�܂���B��̓I�ɂ́C���őS�̂ɐ���������,��@�P����T�܂ł̃q���g�̎�(�v�_���܂Ƃ߂�����)�Ɖp����z������ȉ��ɁC��@�P����X�y�уq���g�Ƃ��Ĕz�z�����\�������B�@��@�P�E���`�a�b�̏��Ŏ��`�}��S��(64�ʂ�)�����Ă���ԋʂ��܂ނ��̂�������B �@��@�Q�E�ԋʂ��ǂꂩ�P�̔��ɓ���Ă���l����B �@��@�R�E�R�̔��ɐԋʂ��R�����ꍇ�C�Q�����ꍇ�C�P�����ꍇ�ɕ�����B �@��@�S�E�S�̂���ԋʂ��P������Ȃ��ꍇ�������Ɛԋʂ����Ȃ��Ƃ��P�����Ƃ��������ɂȂ�ƍl���ĉ����B �@��@�T�E���`�a�b�̏��ɋʂ�����ƍl���C�ԋʂ��ŏ��ɓ���锠���w�肵�čl����B �@��@�U�E���`�a�b���S�F�̐F���M�œh�蕪���ē������߂�B �@��@�V�E���`�a�b�̏��Ɏ��`�}�������B�ԋʂ��܂ސ}�݂̂������o�� �@��@�W�E�R�̔��ɓ����ʂ̎�ނ̐�����Ƃ��čl����B �@��@�X�E�ʂ�F���Ƃɐ����ɒu�������C���̐ς��l����B�ԋʂ��O�Ƃ����ꍇ�C���`�a�b�̐ς͂O�ɂȂ�B�܂�Ԃ������Ă���Ƃ��͂O�ɂȂ�B |
|||||||||||||||||||||||||||||||||||||||||||
| �@ | �E | �@�O���[�v���Ƃ̊����̎w���y�ѐF���M�C���͂����Ɖp���̔z�z | |||||||||||||||||||||||||||||||||||||||||||
| �@ | �@ | �@�P�N���X37�l���U�l�̔ǂT�ƁC�V�l�̔ǂP�ɕ����C�ǒ������߂Ă����B����ɁC�P�̔ǂ��Q�l���R�̃O���[�v�ɕ������B(�V�l�̔ǂ݂̂R�l�̃O���[�v���P�o����B)���̍ہC���ԓ��Ŋe�ǂ���@�P����T�ɂP�ʂ���g�߂�悤��,�O��������Ң��@�P�Q�R�S�T�̏��ʼn�����C��납������Ң��@�T�S�R�Q�P�̏��ʼn�����C�^��������Ң��@�R�S�T�P�Q�̏��ʼn�����Ƃ����悤�ɕ������B������,���Ԑ�̎��ɂ͉������l�ɐ������Ă��炤�悤�ɂ����B �@�܂��C���f���Ƃ��Ĕ��`�a�b�̑���ɉ�p����p�ӂ��C�ʂ̑���ɂ��͂����ɐԔ����̃V�[�����͂�������(�Q�Z�b�g)�ƐF���M(�Ԕ���)���P�{���z�z�����B�����̎g�p�ɂ��Ă͎w���͈�������k�B�̎��R�ɂ������B����ɁC�p���͌�ŃO���[�v���Ŕ�r�������₷���悤�ɉ�@���Ƃɉ����w�������B���@�ɂ��Ă����R�ɂ������B |
|||||||||||||||||||||||||||||||||||||||||||
| �@ | �G | �@���̔z�z�Ǝ��Ƃ̂܂Ƃ�(�`�F�b�N�V�[�g�ƃA���P�[�g) | |||||||||||||||||||||||||||||||||||||||||||
| �@ | �@ | �@�܂��C��(64�ʂ�̎��`�}�Ƃ������J���[�v�����g���Ĉꗗ�\�ɂ�������)��z�z������C�`�F�b�N�V�[�g��z�z���C���ꂼ��̉�@�̊��z�������悤�Ɏw�������B�����C�����������Ă��Ȃ���@������Ή������l�ɐ������Ă��炢���̈�ۂ������悤�Ɏw�������B���̌�C����̎��Ƃɂ��ẴA���P�[�g���Ƃ�C�ǒ��ɔǂ̈ӌ����܂Ƃ߂�悤�Ɏw�������B�e�ǒ����ӌ����܂Ƃߔ��\���C�S�̂ō���̎��Ƃ̂܂Ƃ߂�����B | |||||||||||||||||||||||||||||||||||||||||||
| (3) | �@���Ƃ̓W�J | ||||||||||||||||||||||||||||||||||||||||||||
| �@ | �A | �@�P�����@���̏��� | |||||||||||||||||||||||||||||||||||||||||||
| �@ | �C | �@�w�K�v�� | |||||||||||||||||||||||||||||||||||||||||||
| �@ | �@ | �@����Ƒg����(15����)�@����(7����)�C�A�g����(7����)�C�܂Ƃ�(1����)�c�{�� | |||||||||||||||||||||||||||||||||||||||||||
| �@ | �E | �@�ڕW | |||||||||||||||||||||||||||||||||||||||||||
| �@ | �@ | �@����g�����̂܂Ƃ߂Ƃ��āC����܂Ŋw�K�������Ƃ����ƂɁC1�̖������낢��ȕ��@�ʼn����C���ꂼ��̉�@�̂悳���l����B�܂��C�O���[�v�ł̍�Ƃ�f�B�X�J�b�V������ʂ��āC���w�I�����̊y�����𖡂키�B | |||||||||||||||||||||||||||||||||||||||||||
| �@ | �G | �@���� | |||||||||||||||||||||||||||||||||||||||||||
| �@ | �@ | �@���ȏ��C�m�[�g�C���W�C�v�����g�C�}�O�l�b�g�V�[�g�i�ԁC���C�C���R���j�C�F���M�C�F��p���R���(���`�a�b�̃��f��),���͂���(�ԁC���C�C���R�����e�ǂɕ�����) | |||||||||||||||||||||||||||||||||||||||||||
| �@ | �I | �@�w�K�w���ā@ | |||||||||||||||||||||||||||||||||||||||||||
| �@ | �@ |
|
|||||||||||||||||||||||||||||||||||||||||||
| (4) | �@���Ƃ̍l�@ | ||||||||||||||||||||||||||||||||||||||||||||
| �@ |  �@�܂��C���̈Ӗ��̊m�F���邽�߁C�ԋʂ��K������Ƃ������������Ȃ��ꍇ�̋ʂ̓�����̑���������������k����͂R�̓�12�o3�C12�b3�C43���ł���,���̈Ӗ����m�F���Ȃ���43�����ł��闝�R����������B���ɁC�ǒ������@�̃A�C�f�A�\�������B�����炩��C�p�ӂ����X�̉�@�̓��C���k���炠�������A�C�f�A�͉�@�P�Q�R�S�̂S�������(��@�Ƃ��Ă�����Ȃ��������̂ɂ��ẮC�����炩����������)�����āC�ǂ��Ƃɉ�@�P����T�Ɏ��g�ނ悤�Ɏw�������B �@�܂��C���̈Ӗ��̊m�F���邽�߁C�ԋʂ��K������Ƃ������������Ȃ��ꍇ�̋ʂ̓�����̑���������������k����͂R�̓�12�o3�C12�b3�C43���ł���,���̈Ӗ����m�F���Ȃ���43�����ł��闝�R����������B���ɁC�ǒ������@�̃A�C�f�A�\�������B�����炩��C�p�ӂ����X�̉�@�̓��C���k���炠�������A�C�f�A�͉�@�P�Q�R�S�̂S�������(��@�Ƃ��Ă�����Ȃ��������̂ɂ��ẮC�����炩����������)�����āC�ǂ��Ƃɉ�@�P����T�Ɏ��g�ނ悤�Ɏw�������B�@�e�ǂł̊����ł́C�����ʼn����Ă��瑼�̐l�ɐ���������́C���͂������Ŏ�������@�̈Ӗ����m�F���Ȃ���������̂Ȃǂ��낢�댩��ꂽ�B �@��@�P�ɂ��Ă͐F���M�𗘗p���ĉ����Ă�����̂������C�S�������o���������̕������������o������(��@�V)�����������B��@�Q�ɂ��Ă͕\���������܂��Ȃ��߂��������Ă��܂������̂���������ꂽ�B���̗�͐��k�Ƀ_�u���J�E���g���l���������ŏd�v�ȉ�@�ł��������C���g���k���S�C�T�l�������炸�C���g�܂��邽�߂̗U�����@���H�v���ׂ����Ɗ������B��@�R�ɂ��ẮC�������Ă���v�Z���ċ��߂���̂����������B��@�S�ɂ��ẮC�v�Z�݂̂łS�R�|�R�R�Ƃ��ē����o�����̂����������B���w�����ӂȐ��k�͂����Ɍv�Z�ʼn����͂��߂����C���Ȑ��k�͎���������C���k���Ă�������Ă���̂������I�������B��@�T�ɂ��ẮC��̓I�ɑS���������o���ĉ������ҁC�r���őS�������o�������v�Z�ɐ肩�������������Ɣ��f���Čv�Z�ɐ�ւ����ҁC�ꍇ�킯���ƂɌv�Z�ʼn������ҁC�Ȃǂ��낢��ɕ����ꂽ�B��20���ԂŎ��g��@���͕��ς��ĂR�ł���,���łࢉ�@�R�v��������n�߂��O���[�v�������̉�@�Ɏ��g�ނ��Ƃ��o�����B����́C��@�R�ƂS���Z�b�g�Ŏ��g�߂�����ł��낤�B �@�e��@�ɂ��Ă̊��z�̒��ŁC���`�}�ɂ���@�P�ɂ��Ă͊m���ȕ��@�ł͂�����̂̎��Ԃ��������đ�ς��Ɗ����Ă��鐶�k�����������̂������I������� �@��@�Q�ɂ��Ă�,��\�������ۓI�ŋ�̓I�ɂǂ�����悢�������炸�������Ă��܂������Ƃ������z�����������B�����ŁC���j�����������Ԃ����X���Ă��܂����҂������������Ƃ����������B���������k���o���������͂�����̗\�z�ʂ�48�ʂ�ł��������C�_�u���J�E���g����ꍇ�̗�܂ŕ��������̂͂Q�l(�P�O���[�v)�����������B��@�R�C�S�ɂ��ẮC��@�S��������Ή�@ �R�͂��K�v���Ȃ��Ƃ����ӌ������������B����,���@�T�����@�P�ցv�����Ă������O���[�v�ɂ��̈ӌ������������B����́C��@�S�̕����v�Z��������Ȃ����ƁC�܂������ȒP�Ȃ��Ƃ���l����Ǝ��R�Ȃ��Ƃ��Ǝv����B��@�T�́C�����Ă݂���ӊO�ƊȒP�������Ƃ������z�������݂�ꂽ�B����́C���͂����ŋ�̓I�Ɏ������邱�Ƃɂ���ĉ�@�̈Ӗ��Ɏ��������Ă����߂ł��낤�B �@�A���P�[�g���ʕ\�S���݂ĕ�����悤�ɁC�O���[�v�ł̘b�������ɂ����Ƃł́C��@�̗�����s�������Ȃǂ��ł��Đ��������悤�Ɏv����B��@�𗝉����Ă��鐶�k�͎����̍l�����m�F����Ӗ����܂߁C���͂������g������}���������肵�āC�܂��������Ă��Ȃ����k�ɔ[�������܂Ő������Ă����̂���ۓI�ł������B���̂悤�Ɏ����Ŗ��̈Ӗ����@��[�����Ă�������Ƃ����_���u�`�`���ƈ��������̎��Ƃ̂悳�ł��낤�B�����āC���k���悢�Ǝv����@�Ƃ��ĉ�@�P�ƂT�����������̂́C��̐�������C�������������������ďo�������Ƃ��v���ł���悤�Ɏv����B |
||||||||||||||||||||||||||||||||||||||||||||
| �@ | �\�S�@�A���P�[�g�̓��e�ƌ��ʂɂ��āi�����l��37�l�j
|
||||||||||||||||||||||||||||||||||||||||||||
| (5) | �@�܂Ƃ߂ƍ���̉ۑ� | ||||||||||||||||||||||||||||||||||||||||||||
| �@ | �@���z�̒��ɢ����Ȃɑ����̉�@������Ƃ͎v��Ȃ���������������B���i�̎��Ƃł͎��ԁ@�I���������C�ʉ����������Ƃ��炢�łX��(�܂��͂���ȏ�)�̉�@�����낤�Ƃ͎v��Ȃ������悤���B����̎��ƌ����́C�������o�����Ƃ������낢��ȉ�@���s�����Ƃɂ���ėl�X�Ȑ��w�I�����̊y�������������邱�Ƃɂ���̂œ����̖ړI�͒B�����ꂽ�Ǝv�����B�܂��C���w�ɋ��ӎ��������Ă��鐶�k����u�����ɂ���������@�������Ă悩�����v�Ƃ������z���o���ꂽ�B���i�̎��Ƃł́C���t�����҂����@�����S�ƂȂ邪�C�{���Ƃł͉�@�̃A�C�f�A�̃q���g��^����ȊO�͐��k�̎��含�ɔC�����̂ŁC���k�͎������g�̃��x���ƃy�[�X�ŐS���I���S���Ȃ��C�L�ѐL�тƎ��g�߂��悤���B�����āC�����Ő������o������т́C����̐��w�I�������s���Ă�����Ŏ��M�Ƃ��C�������炵���Ƃ����_�ő�ψӋ`���������B���̂悤�ɁC�����̗����ł��郌�x��������g�݁C�F�l�Ƃ̃R�~���j�P�[�V������ʂ��ĕʂ̉�@�⍂�x�ȉ�@�Ɏ��g�ނ��������ƂȂ�C���w�I�����͂���w�y�������̂ƂȂ�C����w�ю���l����w�K�����ւ̏d�v�ȑ�������ɂȂ�Ɗ������B �@�����āC���k�̉⊴�z���犴�������Ƃ́C������@�P���Ƃ��Ă����k�̐��w�I�\�͂�o���ɂ���Ă��܂��܂Ȍ��������Ă���C�K���������t�̑z������C���[�W�Ƃ͈�v���Ă��Ȃ����Ƃł���B�w�����@�ɂ��āC���k�̏����Ȃ���C�₦���H�v����P�����Ă������Ƃ̕K�v�������߂Ċ������B���ꂪ������g�ނׂ��ۑ�ƂȂ�悤�Ɏv�����B |
||||||||||||||||||||||||||||||||||||||||||||