【授業研究１】

第２学年　基本の運動（ダンボール跳び）

（１）	授業研究のねらい
	第１・２学年の基本の運動の内容は，走・跳の運動遊び，力試しの運動遊びなどの各種の運動遊びについて，仲間との競争，いろいろな課題への取り組みなどを楽しく行うとともに，体の基本的な動きや各種の運動の基礎となる動きができるようにすることである。走・跳の運動遊びでは，多様な走，跳の運動遊びを，楽しく行うことをねらいとしている。 　今回取り上げた「ダンボール跳び」は，いろいろな形に積み上げたダンボール箱をいろいろな跳び方で跳び越すことを楽しむ運動遊びである。ダンボール箱には当たっても痛くない，崩してもかまわないという特徴がある。「ダンボール跳び」を教材とした時には，跳び越す時の踏み切り方，空中姿勢，着地の姿勢などの工夫が容易に行えると考えられる。また，ダンボール箱の置き方の工夫も考えられる。 自分なりに考えた跳び越し方（空中姿勢）だけを「工夫」と考えるのではなく，「助走の距離はこうしよう」「腕はこう動かそう」「ここで踏み切ろう」といった動きの工夫も「児童の工夫」と考えたい。 このように，工夫しやすい条件を持つ「ダンボール跳び」という運動教材を採用し，児童が工夫したことを教師が積極的に賞賛し，児童相互に認め合う場を設定することで，「こんな跳び方をしてみたい」，「次はこうしてみよう」という児童の願いを大切にし，しかも，「できた」，「跳べた」という楽しさが味わえる授業が展開できると考えた。
（２）	仮説について
	仮　　　　説 検　　　　　　　証 １ 　工夫した動きを発表し合う場を「練習―ミニ発表会―練習」というサイクルで設ければ，児童は友達とのかかわり合いの中で，動きの工夫や動きの発見をすることができるであろう。 　ビデオから，跳び越し方の数をカウントし，ミニ発表会前と後の跳び越し方の数を比較する。 　ミニ発表会後のほうが跳び越し方の数が増えているであろう。 ２ 　教師の意図的な指名で全員の前で発表する機会を設ければ，発表を体験した児童は工夫をするであろう。 　発表した児童の跳び越し方の数をカードからカウントし，発表前と後の数を比較する。 　発表の場を体験した後のほうが，跳び越し方の数が増えるであろう。 ３ 　工夫して運動した児童を賞賛するカードを教室に掲示すれば，児童は工夫して運動するであろう。 　掲示された児童の跳び越し方の数をカードからカウントする。掲示される前と後の跳びこし方の数の平均値を比較する。 　掲示された児童は，跳び越し方の数が増えるであろう。 ４ 　ダンボール箱という，軽くて場の工夫が容易で，ぶつかっても痛くなくい教材を用意することで，児童は工夫して運動を行うであろう。 　第１時と第５時に，自由に跳び越させる。跳び越し方の数をビデオからカウントする。 　ダンボール箱を使用した今回の授業は，児童の工夫を引き出し，第１時よりも第５時の方が跳び越し方の数が多くなるであろう。
（３）	授業実践
（４）	授業実践のまとめ
	ア	授業分析と考察
		本実践は，小学校第２学年の２クラスで行った。２クラスとも同じ学習過程,場の設定で実践した。跳び越し方の数え方は，表１の分類に従って行った。
	表１　跳び越し方の分類 助走のしかた 踏み切り足 空中姿勢 空中でのひねり 普通の走り 後ろ向き走り スキップ カニ走り 片足踏み切り 両足踏み切り 前後開脚 左右開脚 前方に足をｖ字に開く 前方に両足キック 空中で自転車こぎ 幅跳びのそり跳び ハードル跳び 抱え込み 伸身 なし ４５°ひねり ９０°ひねり １８０°ひねり
		（ア）	仮説１について
			第２時，第３時のめあて�@の「練習―ミニ発表会―練習」における児童の跳び越し方の数をビデオからカウントしたものが表２である。
			表２　発表会の前後の跳び越し方の数 　 ２年１組 ２年２組 第２時 第３時 第２時 第３時 ミニ発表会の前 　８ 　９ 　９ 　６ ミニ発表会の後 １２ １２ １５ １０
			発表会の後の方が跳び越し方の数が多い。「練習―ミニ発表会―練習」というサイクルを設けたことで，友達の跳び方を参考にし，そこから，自分なりの跳び越し方を考えたからだと思われる。跳び越し方をみると，ひねり動作を加えた工夫が多くみられた。
		（イ）	仮説２について
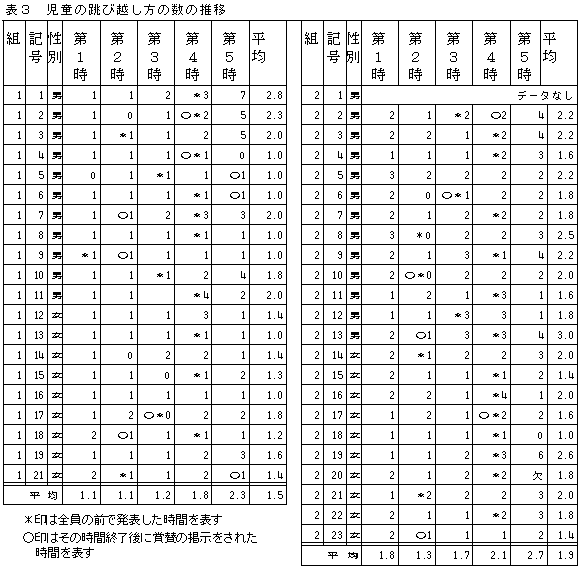
			第１時から第５時までの跳び越し方の数をカードからカウントしたものが，表３である。
			全員の前で発表する機会を得る前と，発表した後の跳び越し方の数の違いを，平均値で表したのが表４である。全員の前で発表する機会を得た後の方が，跳び越し方の数が増えていることがわかる。全員の前で，発表することが，児童の工夫を引き出すのに有効であったと考えられる。
	全員の前での発表の様子
		（ウ）	仮説３について
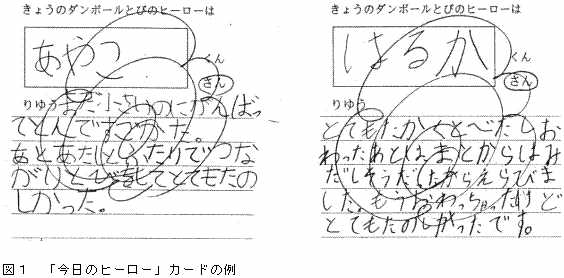
			毎時間終了時に，「今日いちばん工夫していた友達」を選び，「今日のヒーロー」というカードに記入させた（図１）。回収し選択数の上位１〜２名を学年の廊下に掲示した。
			掲示された児童を抽出し，掲示される前と掲示された後の１時間あたりの跳び越し方の数の平均値を比較したものが表５である。 　賞賛の掲示をされた後の方が跳び越し方の数が多くなっている。児童の様子を観察して感じたことは，賞賛の掲示によって，もっといろいろな跳び越し方をしようという向上心につながり，そこから児童の工夫を引き出すことができたのではないかということである。
		（エ）	仮説４について
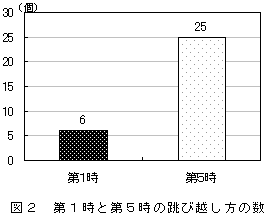			第１時と第５時とでは，ダンボール箱の跳び越し方の数に違いがあるか検討した。跳び越し方の数をビデオからカウントしたものが図２である。この図を見ると，第５時の方が大幅に跳び越し方の数が増えていることが分かる。跳び越し方の内容をみても，バラエティーに富んだ跳び方が，数多く出ていた。 ダンボール跳びといった今回の授業は，児童の跳び越し方の工夫を引き出すのに有効であったと考えられる。
		（オ）	児童の自己評価カードから
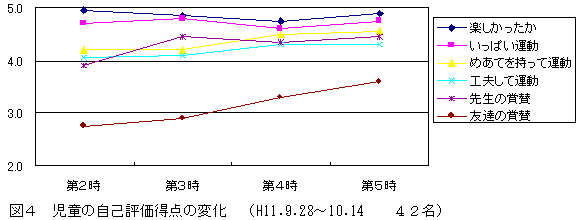
			毎時間の終了時に，図３のようなカードを使って，それぞれの項目を５段階の尺度で評価させた。第２時から第５時までの毎時間の評価得点の変化を表したものが図４である。 　「めあてを持って運動した」，「工夫して運動した」，「友達からほめられた」という項目が時間を追うにつれて同様の傾向を示しながら上昇していった。 　児童が工夫して運動するためには，具体的なめあてを持たせること，友達との認め合いの場を設定することが必要であると考えられる。
	イ	成果と今後の課題
		（ア）	今回の実践では，ダンボール箱を活用したことが児童の工夫を引き出すきっかけになったと考えられる。ダンボール箱を跳ぶという単純な運動の繰り返しにもかかわらず児童は驚くほど熱中して運動していた。 　それは，「ぶつかっても痛くない」，「箱の配置を自由に変えられる」，｢崩してもかまわない｣といった教材としてのダンボール箱の持つ特徴が，児童の「こんな跳び方をしてみたい」，「○個のダンボール箱を跳び越してみたい」という願いを引き出したと授業後の感想から感じ取れた。 　また，自分の跳び方を友達に認めてもらう，誉めてもらう機会を多く設定したことが児童の工夫への意欲を高めることにもなったと考えられる。 　このように単純で自由度の高い教材の採用と児童相互の認め合い励まし合う機会の設定で児童の工夫を引き出すことができたと考えられる。 　また，40項目にわたるアンケートを単元前と単元終了後に実施した。その結果から，特に変容が認められた項目を表７に示した。 　２回のアンケートの結果から，「動きを工夫して運動している」という項目の数値が向上した児童は，「体育の学習は，自分で決めて行動し，自分で評価している」，「できない運動でもあきらめずに練習すればできるようになると思う」という項目も向上していることがわかった。 　以上のことから，第２学年の体育学習において，児童の工夫を引き出すためには，具体的で自己評価が可能なめあてを持たせること，がんばればできると思わせるような場の設定をすることが必要であると考えられる。
			表６　アンケートから変容がみられた項目 （H11.10.14　42名） ・体育の授業で先生からほめられる ・体育の学習で学んだことを取り入れて遊んでいる ・運動している時友達が励ましたり応援してくれる ・運動が上手な見本として，よく選ばれる。 ・動きを工夫して運動している ・自分から進んで取り組んでいる ・体育の授業は冒険しているような楽しみがある ・努力さえすればたいていの運動は上手にできると思う ・一緒に運動しようと誘ってくれる友達がいる
		（イ）	今後の課題
			今回の実践では，児童は驚くほど熱心に運動に取り組んでいた。ただダンボール箱を跳ぶという単純な運動のどこに児童の意欲を引き出すものがあったのかを研究していきたい。 　また，児童の工夫を引き出すための具体的で自己評価が可能なめあての持たせ方，がんばればできると思わせるような場の設定の方法を明らかにしたい。 　今回の実践では，一人一人の跳びこし方の変化を詳しく検証することができなかった。教師の支援や助言が一人一人の児童の跳び越し方の変容とどのような関係にあるのかを明らかにしていきたい。