| 【授業研究３】 | ||||||||||||||
| 高等学校第１学年「不等式の証明」 | ||||||||||||||
| （１） | 授業の構想 | |||||||||||||
| 数学の学習では具体的なイメージで考えると理解しやすい場合が多い。操作的な活動を取り入れることで理解が早まる場合もある。このような活動を繰り返すことにより，まったく別だと考えていた問題とのつながりが見えてくることもある。昨年度の研究により，ある事象に数学的考察を加え，多様な見方や考え方を活かしながら数学的意味を見出すときに，「コンピュータを利用した学習」や「グループによる話し合い」が有効であることは確認されている。本年度は昨年度の研究成果を踏まえ，「模型を利用した学習」を取り入れ，生徒自身がある不等式を拡張して新しい別の不等式を作りだし，それを確かめ証明することができたり思いもよらない原理・法則との関係を見出すことができたりすれば，思考の拡散を生み，創造性の育成につながるものと期待しこの授業を組み立てた。また，ほとんどの不等式にはその成立の背景があり，それらに触れることにより生徒の興味・関心を高めることもできる。具体的には，命題「ａ1>ａ２，ｂ1>ｂ2ならばａ1ｂ1＋ａ２ｂ2>ａ1ｂ2＋ａ２ｂ1である」をてんびんとおもりという簡単な模型を操作して理解してから代数的に証明し，さらにその不等式を発展させる授業を行った。 | ||||||||||||||
| （２） | 指導の手だて | |||||||||||||
| ア |
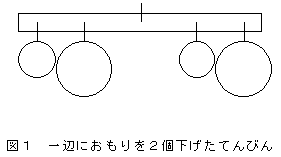学習課題についててんびんは，シーソーなどのように，生徒にとって身近な存在であり，実体験として理解しやすいものである。 だが， ここに条件「同じ重さのおもりを２個ずつ用意し，支点から同距離にある点を左右に取り，これらのおもりを下げる。ただし，左右のおもりの個数及び重さの合計は同じものとする。」を付けることで，つりあわない状態を不等式で表現することができれば，その規則性には面白いものがある。例えば，てんびんの左右におもりを２個ずつ下げたときは，支点からの距離をａ1>ａ２>0，おもりの重さをｂ1>ｂ2>0とすると，てんびんが傾く様子は不等式ａ1ｂ1＋ａ２ｂ2>ａ1ｂ2＋ａ２ｂ1で表すことができる。ここで，おもりの個数を増やし，てんびんのつりあいの状況を不等式で考えると，簡単な数列の積和としての性質なども見えてくる。 |
|||||||||||||
| イ |
模型の活用 てんびんとおもりを使うことで，てんびんの傾く方向，つまり不等式の不等号の向きを体験させ，不等式の性質の考察が進めやすくなるように配慮した。 |
|||||||||||||
| ウ |
ワークシートの活用 実験結果をまとめるものとしてワークシートを用意した。左右のおもりの下げ方を考えると，おもり２個の場合で４通り，おもり３個の場合で36通り考えられるが，この中には他と重複する場合や，つりあうことが明らかな場合もある。これらは考察から除外しても問題ないのだが，今回は，生徒自身がこのような点に気がつくように配慮した。 |
|||||||||||||
| エ |
グループでの話し合い 実験器具の関係で４人ずつの10グループに編成して授業を展開する。 |
|||||||||||||
| オ |
指導の基本方針 実験結果を数式化したり，大小関係も生徒自身に予想させ，不等式の証明に対する興味・関心を高めるように配慮する。 |
|||||||||||||
| （３） | 学習指導案 | |||||||||||||
| ア | 単元名 不等式の証明 | |||||||||||||
| イ | 学習計画（全４時間･･･本時は２・３時間目） | |||||||||||||
| 第１次 | 相加平均・相乗平均 | 第１時 | 『平均』ってなに？ | |||||||||||
| 第２次 | 不等式の拡張（本時） | 第１時 第２時 |
てんびんのつりあいⅠ（公開授業） てんびんのつりあいⅡ |
|||||||||||
| 第３次 | その他の不等式 | 第１時 | その他の不等式 | |||||||||||
| ウ |
目標 てんびんのもつモーメントの性質を利用し，てんびんのつりあわない場合を不等式で考えることで，不等式の意味を考え，不等式に対する興味・関心を養う。また，証明した不等式の規則性を発見し，その不等式を発展させることで，多様な見方や考え方ができる。 |
|||||||||||||
| エ | 学習指導案（以下の指導案で，○は教師からの働きかけ，●は学習者の活動を表す。） | |||||||||||||
 |
||||||||||||||
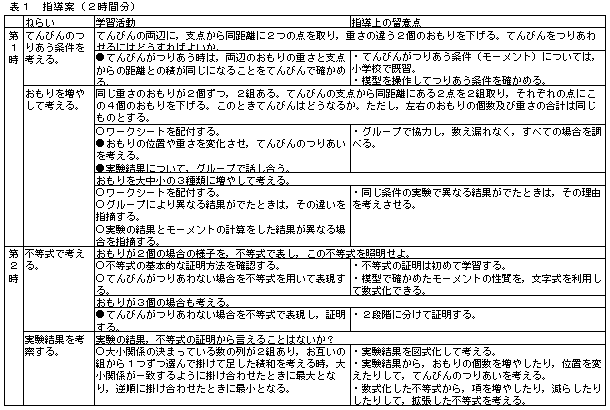| オ |
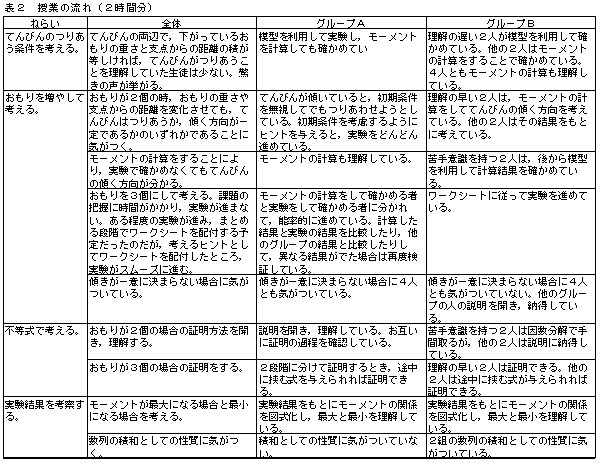
授業の考察研究授業に際して，全体の流れ及び抽出した２グループ（各４人で構成）の様子を観察した。
|
|||||||||||||
 |
||||||||||||||
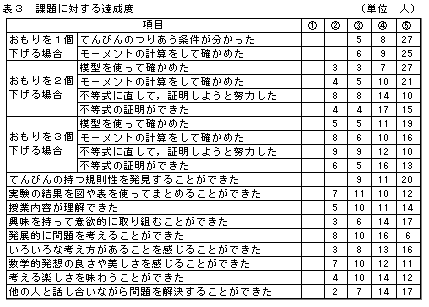第２時終了後、生徒40人に対して、各生徒の課題に対する達成度（表３）及びこの授業に対する感想を調べた。各項目で数字が大きいほど，達成度が高いものとする。導入時に利用したおもりが１個の場合は，達成度の高い方が度数が大きいので，ほぼ全員が理解したと考えられる。ここで，計算によるてんびんの傾きの考え方を確認したので，これ以降の実験でも計算によって確かめる生徒が多かった。そのためか，つりあいが微妙な場合のてんびんの傾きも，計算をすることにより確かめることができた。 模型を使った実験は，グループにより進み具合の差が大きく，全部終了したグループもあれば，半分しか終わらないグループもあった。１時間分を当てたのだが，前半で課題の理解に手間取り，実験そのものが進まなかったためと考えられる。また，「模型で確かめる」及び「計算で確かめる」の２つの項目で度数にばらつきが見られるのは，時間が不足したことも一因であるが，模型が４人に１台しかなく，グループによっては思うように話し合いが進まなかったためとも考えられる。これは「他の人と話し合いながら問題を解決する」で度数にばらつきがあることからも分かる。 第２時の不等式に直して証明する段階は，おもりが２個の場合で全体説明をした上で，３個の場合に取り組ませたが，初めて不等式の証明を学習したということもあり，最初は何をしてよいのか分からない生徒が何人かいた。しかし，２個の場合を数式化して証明すると，ほとんどの生徒がその証明法を理解した。おもりが３個の場合は，直接その不等式を証明することはできないので，間に１つ他の式をはさんで証明するのだが，自分で見つけることができたのは３分の１程度で，他の生徒は具体的にその式をヒントとして与えられて，証明をすることができた。よって，おもりが２個の場合，３個の場合の実験結果の確認及び証明により，てんびんのもつ規則性やモーメントの考え方はほとんどの生徒が理解できたと判断できる。 しかし，実験結果を一般化して考える段階では，モーメントが最大のときと最小のときを見つけることができても，それをうまく説明することはできなかった。「図を使って説明したら」とヒントを与えると，数人の生徒が関係図を完成させ，他の生徒もその関係図や説明のシンプルさに驚いていた。また，第２時の最後に，第１時に実験をして確かめることができなかったおもりが４個の場合の実験結果（全276通り）を表にまとめ配布したのだが，１人の生徒がそれを元に大小関係を表す図をまとめてきた。一部不具合があったので，他数名の生徒と一緒に修正をして再配付したところ，その関係図や模型の美しさ，思いもしなかったものとの関係に，再度驚いていた。 この授業の後，他の不等式の問題を扱ったときに，「この不等式はどんな意味があるの？」という質問が出て，自分たちなりの解釈を試みる態度が見られるようになり，積極的に理解しようという意欲が感じられるようになった。 |
||||||||||||||
| （４） | 研究のまとめと今後の見通し | |||||||||||||
|
本授業は，不等式の証明をほとんど学習していない段階で，ある事象を不等式で表現して，証明し，さらに別の規則性を見つける学習を展開した。不等式の証明に限らず，「数学は何に役立つの？」という疑問はいつでも数学の学習について回る。生徒たちはこの疑問を持ったまま学んでいるわけである。この疑問に対して，誰もが納得するような，はっきりとした答えを出すことは難しい。今回の授業でも「どうしてこんなことをするのだろう」とか「このような授業をすると，今までやってきた数学は何のためにやってきたのかなと思う」という感想もあった。その一方で，「今回の実験や考察で，いろいろな考え方があることが分かり，１つの問題を考えるときに，その先を考えるようになった」，「最初は何か難しくてよく分からなかったけど，結果をまとめていくうちにだんだんといろいろなこと（不等式とてんびん）がつながってきて，どうしてこのような実験をしてきたのか分かった気がする」，「結果の検証や証明はちょっと分かりにくかったけど，あの実験が今やっている計算（不等式の証明）につながっているのがすごい」という肯定的な感想も多かった。 また，「実験をしていて，さらにどのようなことが言えるのか調べてみたいと思った」，「実験結果の中に,自分の考えているものと違った答えが出てきて,考え方が広がった」「自分の予想と結果が違っていたけど，納得がいった」，「初めは何だこれ？と思っていたけど，実験していくうちになぜこうなるのだろうと興味がわいてくる実験だった」という感想に代表されるように，実験から考察にかけての一連の過程を楽しみながら進めている生徒も多かった。これはグループ形態による授業を取り入れたために，生徒の思考活動を促す結果につながったことも１つの原因であると考えられる。ただし，「する人としない人とがでてくる」という感想からも分かるように，より少人数のグループで実験をし，結果を考察する段階でより大きなグループになるといった形態の方が，学習効果が高かったと考えられる。 以上より，身近な事象を数学的に考察することで数学に対する興味・関心を高めることができ，その際に操作的な活動を取り入れれば事象の意味の把握が容易になり，問題に対する多様な見方や考え方を培うことができることが分かった。ただし，非常に難解になる場合もあるので，課題の選択には注意が必要である。 これからも，数学を学ぶ意義が体験でき，多様な見方や考え方が育つ授業の創造に努めていきたい。 |
||||||||||||||