創造性を培う学習指導 - 茨城県教育研修センター

【授業研究１】
	小学校第６学年「対称な図形」
（１）	授業の構想
	これまでに本研究では，問題解決学習における多様な見方や考え方を育てる学習指導を通して望むべき児童の姿を次のようにとらえてきた。児童自身が自ら課題を設定し，解決の見通しを持ち，自由な発想で課題解決を図り，数学的な思考力や考える楽しさを高めていくことである。　資料１は，本校第６学年36人の児童の算数学習に対する意識調査である。　質問１の「算数の学習が楽しいと感じるのはどんな時ですか？」の質問に児童は「問題が解けた時」の解決過程より「答えが正しかった時」の結果の方を重視していることが分かる。　このことは，算数は考える力を育成していこうとすることを主眼とした教科であるにもかかわらず，結果にこだわっている児童の傾向を示している。　質問２，３の課題解決学習における多様な解き方と答えの数についての質問では，解き方については多様な方法があると感じながらも，答えは必ずといっていいほど一つであると感じている児童が多いことが分かる。　質問４の学習した内容を覚えることについての質問では，算数の学習は覚えることがたくさんあると感じている児童がほとんどであることが分かる。解決に必要な事項を選択したり，類推して関連づけて考えたりするよりも，解決方法を覚えて，安心してしまう思考の傾向がある。以上の結果から，児童は問題を解決さえしてしまえば，そこで学習が終わってしまうのである。きまりや公式は覚えてしまえばよいといった態度が身に付いてしまい，算数本来のもつおもしろさや不思議さを感得できなかったり，解決に用いた数学的な見方や考え方の有用性を十分に意識できなかったりしているように思える。　このような実態を改善していくためには，解答方法や求め方がいく通りにも可能になるような学習問題を設定し，課題解決学習に取り組んでいくことが有効な学習方法として考えられる。これらの学習を通じて多様な見方や考え方が育ち，論理的な思考力・直観力・想像力を少しずつ身に付けていき，児童生徒の創造性を培っていきたいと考えた。
（２）	指導の手だて
	ア	単元について　本単元では，図形を弁別したり統合したりする観点として対称の概念を導入し，図形を新たな観点でとらえていくことをねらいとしている。　線対称と点対称の共通点は，①共に１８０度の移動であること。②同じ距離で図形の頂点や辺や角が対応していること等が挙げられる。さらに線対称と点対称の図形を見たり作図したりすると児童の反応として「二つの図形の関係がきれいだ」，「形が整っている」，「バランスがよい」，「美しい」等の感覚がうまれる。美的な感覚やセンスは人それぞれであるが，共通する根拠の一つに対称性がある。すなわち,180度の移動と点や辺の同じ距離の対応という図形の見方が図形に対する美的な感覚を生み育てることに役立つといえる。　今回の学習指導要領の改訂により，本単元の学習内容は中学校１年に移行されることとなっている。しかし，児童自らが線対称や点対称の共通点に着目することで両者を統合的に見る見方に気づき，図形に対する豊かな感覚を創造できるという本単元を学習する価値は非常に大きいと考える。
	イ	指導に当たって
		（ア）	数学的な直観力を育て，多様な見方や考え方を育てる指導方法の工夫を図る。児童の自由な発想や考えが可能な学習場面を考える。　児童の実態から，児童一人一人の自由な発想や考えを可能にするためには，解答がいくつもあり，それに伴って複数の解決方法が考えられる学習課題の設定が必要である。そこで，研究授業ではオープンエンドの問題（Open end problem）を学習課題に用いる。また，児童の五感が働く場の設定も学習場面の工夫では重要な要素の一つと考えられるので，平成10年12月に告示された新学習指導要領解説算数編の目標の「算数的活動」を重視していきたいと考える。その「算数的活動」の中から，本研究では体験的な算数的活動と応用的な算数的活動を研究授業の中に取り入れることにする。児童の数学的な見方や考え方のよさを認める。　数学的な見方や考え方のよさを認め合うためには，学習形態の工夫が必要である。本単元では，６時間の学習でコンピュータを活用する場面を考え，授業研究でもコンピュータを活用する。このときの有効な形態として，二人ずつのペア学習の形態をとることにした。また，コンピュータを互いの考えを共有する場として活用し，ペア同士，ペア以外の友達同士，児童と教師の相互の認め合いの場面を作りたいと考える。十分な学習活動時間の確保をする。　十分な学習活動時間の確保をするために，学習課題の提示の効率化を図りたい。そのためには，各単位時間に何を学習するのか，単元の導入段階で単元の学習内容や学習方法を見通す学習活動を取り入れ，どの授業も見通しを持ちながら学習に望むようにすることにする。課題提示や課題把握の場面での時間の短縮が図れ，自力解決や集団解決での学習活動時間の確保を図る。
		（イ）	多様な数学的な見方や考え方を基に練り上げ，論理的な思考力を育てる指導過程の工夫を図る。着想したことや考えたことを表現する学習過程を作る。　本単元では，自分の考えを表現する活動として，対称な図形の作図があげられる。フリーハンドで簡略化してかく場合や定規で正確にかく場合など授業展開に応じて様々な表現方法を取っている。　その中に，今回はコンピュータ（図形ソフト）の活用方法を考え，単元の学習過程の中に意図的に位置づける。コンピュータによる作図の長所（映像性，動画性，即時性，記憶性等）を生かして，児童の数学的な表現活動の幅を広げたいと考える。互いの解決方法を認め，問い直すことから一般化・統合化を図る。　集団解決の場面では互いの解決方法を認め合い，考え方のよさを手がかりにして一般化や統合化を図っていく。授業研究は，単元の終末場面であるので,｢どうして対称な形が，きれいで，形が整ったものとして見えるのか」を考えることから，図形の特徴や性質を再度振り返るとともにその美しさに触れ，関心を高める。
（３）	授業の展開
	ア	単元名　　対称な図形
	イ	学習計画　（11時間取り扱い）

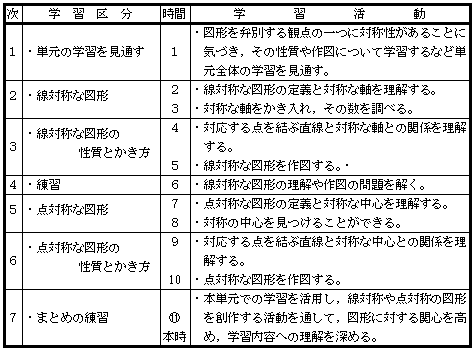	ウ	本時の目標対称な図形の性質に帰着しながら，図形のもつ機能性や美しさを感得することができる。体験的な算数的活動を通して，対称な図形の性質やかき方についての理解を深めることができる。
	エ	準備・資料ワークシート，定規，コンピュータ（使用ソフト：創育　算数ランチボックス２）
	オ	展開

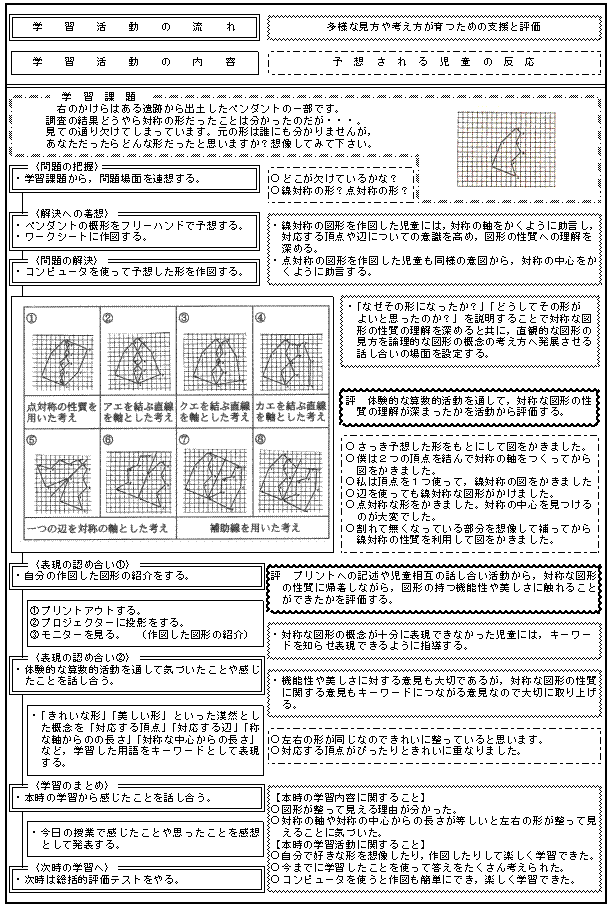（４）	授業の記録と考察
	資料２　学習問題に対する児童の解答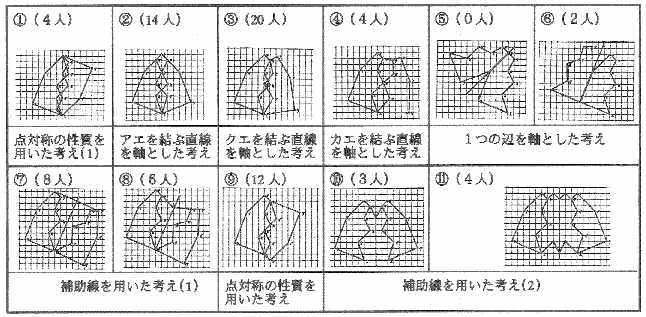
	ア	対称な図形の性質の理解　本時の学習問題は，オープンエンドの問題を用いたため，児童は直観的に様々な解決の見通しを持つことができた。児童全員がフリーハンドや定規を使ってペンダントの形を想像しワークシートに表現できた。それは，本単元の導入段階で学習内容や学習方法の見通しを持つ学習計画作りをした結果，本時の問題解決の見通しを図る時間を十分に確保できたためであると考えられる。見通しを十分に持つことで，資料２にあるように，児童が直観力や想像力を働かせながら多様に考えることができた。
	イ	図形のもつ機能性や美しさに触れる　児童の感想から，「どの図形も左右のバランスがよくきれいに見える。」「人は対称な整った形を無意識に好むんだなーと思った。」等の意見が出された。プロジェクターでの図形の操作の投影が，辺や頂点の位置関係に着目する視点を明確にししたことは，論理的な思考力の手助けとなった。児童は図形のもつ美しさに触れられたようである。
（５）	まとめと今後の課題
	問題解決学習における多様な見方や考え方を育てる学習指導として，オープンエンドの問題を解決していく学習活動に取り組み，児童の多様な見方や考え方を認めることができた。また，教師の支援や児童の相互援助により直観力や想像力，論理的な思考力を高めていくことができた。今後は，これら多様な見方や考え方をどのように評価し，どのように練り上げよりよい見方や考え方に高めていくか。また，高められた見方や考え方を児童がどのようにその見方や考え方を活用していったらよいかをを検討していきたい。