| はじめに |
|
これからの社会においては，自ら学ぶ意欲と社会の変化に主体的に対応出来る資質が求められている。そこで必要とされている資質は，知識や技能ばかりでなく，日常生活の中で生きて働き，必要な場面で進んで活用できる能力として身に付けられたものである。特に，算数・数学教育においては，基礎的・基本的な内容の確かな定着を図るとともに，創造的活動をするための基礎となる論理的な思考力や直観力の育成が必要である。そこで，算数・数学科の学習指導では，問題解決のための多様なアイディアを直観的に創造する力を育てたり，問題解決の方法を論理的に表現する力を高めたり，数学的な見方や考え方のよさを感じたり できるような児童生徒を育てることが大切であると考える。 |
| |
|
| １ |
研究のねらい |
| |
問題解決学習において，「多様な見方や考え方を発見するまでの数学的な直観力にかかわる学習の工夫」や「多様な見方や考え方を生かして，話し合い，論理的な思考力を育てる学習にかかわる工夫」などの研究の視点を設定し，創造性に関する意識・実態調査を踏まえながら,｢多様な見方や考え方を育てる学習指導」における学習過程や学習指導の在り方について究明する。 |
| |
|
| ２ |
研究主題に関する基本的な考え方 |
| |
（１） |
研究主題と学習指導要領との関係
文部省告示175，176号（平成10年12月14日）で発表された小学校・中学校新学習指導要領について見ると，算数，数学それぞれの第３節 第１目標に「数量や図形についての算数的活動を通して」，「活動の楽しさや数学的な見方や考え方のよさに気付き」，「数学的活動の楽しさ，数学的な見方や考え方のよさを知り」があり，現行の指導要領算数・数学科の目標にはない「楽しさ」という文言を加え新指導要領の特徴を示している。また，高等学校の目標には，「創造性の基礎を培う」が示されている。このことを算数・数学の学習活動の中で考えると，児童生徒が課題をもち，問いを発し，予想を立て，実験をし，論理的に考えるなどの「算数・数学をする」ということを通して，「楽しさ｣ を感得できるようになることが大切であると考えられる。問題を解決していく過程で，一人一人の児童生徒が既有の知識や方法を基に，多様な見方や考え方を想像的・直観的に発想したり，多様な見方や考え方を基にして一般化したり統合化したり発展させたりするときに｢ 楽しさ｣ を感得できるようになると考える。
したがって，児童生徒の多様な見方や考え方を育てることや一人一人の児童生徒の考え・解決方法を生かす学習を組み立てながら，自ら考え問題解決する力を育成することは，新学習指導要領の算数・数学の目標に沿うものと考える。 |
| |
|
| ３ |
算数・数学科における「多様な見方や考え方」に関する意識・実態調査 |
| |
県内の小学校・中学校及び高等学校の児童生徒及び教師を対象として，算数･数学科の｢多
様な見方や考え方」に関する学習指導について意識・実態調査を実施した。 |
| |
（１） |
調査対象 |
| |
|
ア |
児童生徒 |
…… |
校種別に学校規模や地域性を考慮して，調査校を抽出した。抽出した小学校の児童数は480人で県内全小学校児童数の0.5％，中学校の生徒数は1326人で県内全中学校の生徒数の 1.2％，高等学校の生徒数は1158人で県内全高等学校生徒数の1.5％である。 |
| |
|
イ |
教師 |
…… |
児童生徒の調査対象として抽出した小学校・中学校及び高等学校の算数・数学担当者を対象とした。抽出した小学校の教師数は 107人で県内全小学校教師数の 1.3％,中学校の教師数は41人で県内全中学校教師数の0.8％，高等学校の教師数は63人で全高等学校教師数の1.3％である。 |
| |
（２） |
実施時期 平成10年９月25日から10月９日まで |
| |
（３） |
集計結果の分析と考察 |
| |
|
- 算数・数学学習に関する調査項目数は，教師と児童生徒に対してそれぞれ５項目とした。
- 児童生徒及び教師への質問内容は同一のものを考えた。
- 調査項目ア〜オについての質問を枠内に示し，その結果を表１〜５に示した。
- 表中の数値は各問毎の回答者数に対する回答数の割合（％）である。
|
|
| 【以下，質問内容の抜粋と集計結果の分析と考察を掲載】 |
| ア |
多様な見方や考え方（小学生，高校生及び教師用の質問は省略） |
 |
| |
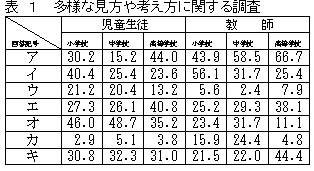多様な見方や考え方については，教師は「ア 教師が課題設定を工夫したとき」に出やすいと高等学校，中学校，小学校の校種別順に割合が高いことが分かる。これに対して高等学校生徒の44％が高いが中学校生徒の割合は低い。「イ 授業で実験や操作的な活動が行われたとき」に，小学校児童・教師ともいろいろな考えが出ると考えている。「オ グループで活動したり，話し合ったりするとき」に高・中・小学校の順に児童生徒はいろいろな考えが出やすいと考えているが教師は必ずしもそう考えていない。逆に多様な見方や考え方への評価が低いものとしては，「ウ コンピュータを活用した授業」や「カ ティーム・ティーチングによる授業」を教師も児童生徒もあげている。また,｢キ 机間指導などの支援」については，児童生徒30％以上が期待しているのに対して,小中学校では,教師の割合が低く，高等学校の教師の割合は高いことを示している。
|
| イ |
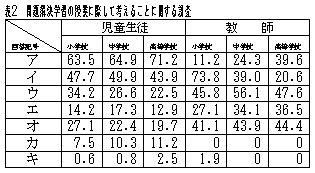
問題解決学習の授業に際して考えること（小学生，高校生及び教師用の質問は省略） |
 |
| |
多様な見方や考え方については，教師は「ア 教師が課題設定を工夫したとき」に出やすいと高等学校，中学校，小学校の校種別順に割合が高いことが分かる。これに対して高等学校生徒の44％が高いが中学校生徒の割合は低い。「イ 授業で実験や操作的な活動が行われたとき」に，小学校児童・教師ともいろいろな考えが出ると考えている。「オ グループで活動したり，話し合ったりするとき」に高・中・小学校の順に児童生徒はいろいろな考えが出やすいと考えているが教師は必ずしもそう考えていない。逆に多様な見方や考え方への評価が低いものとしては，「ウ コンピュータを活用した授業」や「カ ティーム・ティーチングによる授業」を教師も児童生徒もあげている。また,｢キ 机間指導などの支援」については，児童生徒30％以上が期待しているのに対して,小中学校では,教師の割合が低く，高等学校の教師の割合は高いことを示している。
|
| ウ |
数学的な考え方について（小学生，高校生及び教師用の質問は省略） |
 |
| |
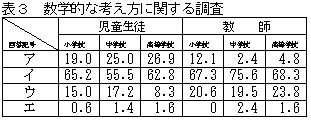問題解決にあたっては，児童生徒も教師も「イ 既習事項の活用を図る」点にもっとも重点をおいている。反対に,｢ア問題の答えや解き方の方法を見通してみようとすること」や「ウ 公式に表したり，関係を言葉で説明したりできるようにすること」に児童生徒はそれほどの関心を示さない，教師においても,｢ア 解答や解決方法を直観的にとらえようとする態度」や「ウ 解決方法をまとめて，一般化しようとする態度」を育てたいとする回答は，あまり多くない。創造性を培うには問題解決にあたっても，ただ単に正解が得られたことに満足するのではなく，そこから得られる事柄を，広く敷衍して考察してみることも重要であり，そういう努力も必要であると考える。 |
| エ |
数学的な見方や考え方のよさについて（小学生，高校生及び教師用の質問は省略）数学的な考え方について（小学生，高校生及び教師用の質問は省略） |
 |
| |
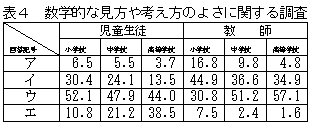数学的な見方や考え方のよさについて児童生徒は｢ウ ときどき｣を，小学校，中学校，高等学校の順に高い割合を示すが，教師は高等学校，中学校，小学校の順で高い。「イ 比較的多く」では，ウの割合ほど高くはないが，小学校児童の30.4％，教師44.9％，ほか，中・高の教師は35％以上のやや高い割合を示している。また，同じこの質問で,｢エ あまりしていない｡｣と回答した教師は極めて少ないが，生徒では中学校21.2％，高等学校38.5％と割合が高く，特に学年が上がるにつれて，その傾向は顕著である。教師側の指導に対する思いと，児童生徒の受け止め方にギャップが感じられる。 |
| オ |
数学的な見方や考え方の内容（小学生，高校生及び教師用の質問は省略） |
 |
| |
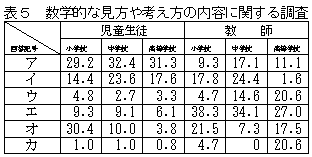数学的な見方や考え方のよさの内容については，児童生徒は,｢ア 公式や筆算などを使って，速く簡単にできた。」で各校種とも30％程度の割合を示しているが，教師は，中学校の17.1％が最高で，高等学校，小学校では10％程度を示している。教師の示す割合は児童生徒ほど高くない。教師では「エ 喜びや楽しさがある。」で小学校，中学校，高等学校の順に多く，児童生徒と比較して，割合が大変高い。「オ 日常生活の中で，学習したことが役に立ち，他に使うことができた」では，小学生，小学校教師に多く，高校生の割合は特に少ない｡小学校で学ぶ算数の内容が,日常の生活に不可欠のものであることの証左と考えられる。｢ウ 美しさや驚きがある｡ ｣では，高等学校教師の割合が20.6％と数値的にはさほどではないが，児童生徒との相対的な比較ではかなり高い割合である。「イ □○△，文字，数字や記号を用いて簡単にまとめたり，公式に表わしたりすることができた」では，中学校生徒，教師の割合が，23.6％，24.4％と高い。また，小学校児童，教師も似た傾向を示しているが，高等学校教師の回答では，相対的に極めて低い割合である。高等学校の数学では文字や記号を用いることが行われているが，改めて文字や記号のよさについて，生徒に考えさせる機会を意識していない傾向にあると想像する。 |
| |
（４） |
調査のまとめ
この調査から，次のことが明らかになった。 |
| |
|
ア |
児童生徒と教師とも，課題内容の工夫，授業で実験や操作的な活動や十分な考える時間があるとき，多様な見方や考え方で問題を解決することができると考えている。またグループで活動したり話合ったりするとき，児童生徒はいろいろな考えが出やすいと考えていることが分かる。さらに，児童生徒は，教師の支援も大切であると回答している割合が高い。 |
| |
|
イ |
問題解決にあたって，児童生徒は解答の正誤に強い関心があるが，教師は考え方や答えについて，自分と他人の相違点を考えるよう指導している割合が小学校の教師に多いことが分かる。 |
| |
|
ウ |
児童生徒と教師とも既習事項の活用を図る点に最も重点をおいているが，問題の答えや解き方の方法を見通してみようとすることや，公式に表したり関係を言葉で説明したりできるようにすることに，児童生徒はそれほどの関心を示していない。同様に教師においても，解答や解決方法を直観的にとらえようとする態度や解決方法をまとめて，一般化しようとする態度を育てたいとする回答は，多くないことが分かった。 |
| |
|
エ |
数学的な見方や考え方と「よさ」について，児童生徒は，ときどき，比較的多く気付いたり感じたりしたことが分かった。また，教師が多様な見方や考え方を育てようと指 導していると回答している割合は比較的多く，ときどきは行っているという回答が多いが，児童生徒が感じている割合は少ない。特に学年が上がると，その傾向は強くなる。教師の指導における考えと児童生徒の受け止め方に差があることが分かった。 |
|
|
オ |
具体的に数学的な見方や考え方のよさを感じる場面として，児童生徒は，公式や筆算などを使って速く簡単にできたことや□○△，文字，数字や記号を用いて簡単にまとめたり，公式に表わしたりすることができたことについて，よさを感じていると回答した割合が高い。一方，教師では，美しさや驚きがあることや喜びや楽しさがあることなどによさがあると思っている割合が高い，児童生徒と比較して，より抽象的なよさを感じていることが分かった。 |
| |
|
| ４ |
研究主題に迫るための手だて |
| |
（１） |
数学的な直観力を育て，多様な見方や考え方を育てる指導方法の工夫 |
| |
|
ア |
児童生徒の自由な発想や考えが可能な学習の場面を考える。
- 児童生徒の五感が働く場（直接的な体験活動や操作的な活動を取り入れた場)を学習活動の中に設定する。
|
| |
|
イ |
児童生徒の見方や考え方のよさを認める。
- 多様な見方や考え方ができるように学習過程,授業形態や支援の在り方を工夫する。
- オープンエンドの問題（Ｏpen end problem ）を学習に活用する。
|
| |
|
ウ |
考えたり操作したりする時間を十分に与える。 |
| |
（２） |
多様な見方や考え方を基に練り上げ，論理的な思考力を育てる学習過程の工夫 |
| |
|
ア |
児童生徒が,問題解決のために着想したことや考えたことを表現する学習過程を構成する。 |
| |
|
イ |
自分の考えや解決方法を児童生徒同士互いに交換することによって,自分の考えや解決方法を問い直し，練り上げる学習過程を構成する。 |
| |
|
ウ |
多様な見方や考え方を基に，論理的・形式的に考えをまとめて,一般化・統合化を図り，活用する場を構成する。
- 一般化・統合化などで得た数学的な見方や考え方をさらに活用することで,考えのよさを感得できるようにする。
|
| |
|
| ５ |
授業研究 |
| |
研究主題「多様な見方や考え方が育つ算数・数学科学習指導の在り方」に基づき,多様な見方や考え方を育むための指導過程や指導の在り方について工夫や手だてを講じ，小学校，中学校及び高等学校各１校で授業研究を行った。 |