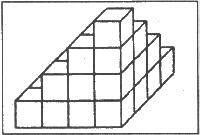
| ア | 教材について 数学Ⅰの「自然数の列」では，三角数・四角数といった図形数を取り扱っている。ｎ番目の二つの同じ三角数の和を考えることで，１からｎまでの自然数の和の公式を導くことは容易で，生徒が公式をイメージするのにも大いに役に立っているものと思われる。ここでは，その図形的な取り扱いをさらに発展させ，数学Ａで代数的に扱った「１からｎまでの２乗の和・３乗の和の公式」を導けることを目標とした。２乗の和・３乗の和を，四角数を積み上げた立体で表す。２乗の和についてはその立体のまま考え，３乗の和についてはその立体を平面に写し，平面上で考える。代数的に導いた公式が，四角数という目に見えるものの和として求めることができれば，生徒たちが数列の和の公式に対してもっている印象も変わってくるであろう。パズル的な要素も含まれ，興味・関心をもって取り組むものと考える。 |
| イ | 前時までの内容 図形数（三角数・四角数）について学習し，それらを用い，１からｎまでの自然数の和，１から２ｎ－１までの奇数の和を求めた。数列を既に学習していることもあって，生徒たちは十分理解できた様子であった。隣り合った三角数の和が四角数になることの発見と，図による説明を次時までの課題として残した。 |
| ウ | 指導に当たって 全員が主体的に課題に取り組めるように，一人一人に資料（発泡スチロールの立体，方眼紙，正方形の紙片）を用意するとともに，活発な意見交換ができるように３人一組のグループ学習とする。最初の課題では「１＋４＋９＋１６」を表す立体を１個与える。この立体は３個を組み合わせるとうまく数えられるようになっており，必要に応じてグループで意見を出し合い，検討できるようにする。次の課題では，四角数を表す正方形の紙とそれを数えるための方眼紙を用意する。一人で考えられるが，お互いの考えを比較検討できるように，グループは維持しておく。公式を求めることができたら，「１からｎまでの３乗の和」が「１からｎまでの和の２乗」になる理由を図で考えることができるようにする。生徒が自力で解決できるように，考える時間を十分にとる。 |
| エ | 学習計画 （５時間 本時は第５時） |
| ア | 目標 四角数の和を立体に置き換えて考えることで，興味・関心をもって課題に取り組み，試行錯誤しながら考えることの楽しさを味わい，数学的な見方や考え方のよさを感得できる。 |
||||||||||||||||||||||||||||||||||||||||||||||||
| イ |
|
||||||||||||||||||||||||||||||||||||||||||||||||
| ウ | 展開
|
||||||||||||||||||||||||||||||||||||||||||||||||
| エ | 授業の記録 研究授業に際して，全体及び抽出した２グループ（３人で構成）の様子を観察した。
|
を求めやすい形に並べてみる。
についても並べてみる。
についても考えてみましょう
