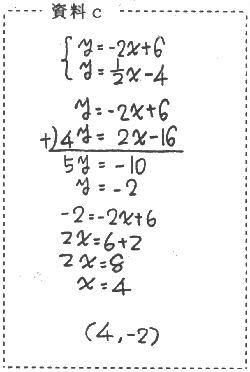【授業研究２】　中学校第２学年「課題学習（『１次関数』）」

１．授業の構想
　中学校第２・３学年で取り扱う課題学習は，課題を含んだ場面を提示することによって，生徒自ら問題となる課題を発見し，既習の学習内容を生かして，その解決に主体的に取り組む学習である。課題学習に取り組むなかで，生徒の課題に対する関心・意欲を引き出すことができれば，生徒は自らの気付きを生かしながら問題を解く楽しさや分かる喜びを感じ，また，数学的な見方や考え方を身に付けながら，豊かな感性が育まれるのではないかと考え，授業研究を行ってみた。
　資料５は本校第２学年「式と計算」の課題学習後の生徒たちの感想をまとめたものである。課題学習の取り組みから，「…楽しかった。」，「…できた。」など，学ぶ楽しさが味わえたという感想が得られた。また，「…難しいが楽しかった。」という感想が多く，課題を含んだ場面の提示の仕方次第では，困難に立ち向かう積極的な態度も育むことができると考えられる。
　そこで，「１次関数」の課題学習を成立させるために，課題を含んだ場面設定の要件，その場面を発展的に見たり考えたりする方法，そして，課題の発見・解決の方法を考え，研究をすすめた。

資料５　初めての課題学習後の感想（１章　式と計算）
平成９年５月２１日実施　２年　１４９人（単位　人）
課題を含んだ場面
「直径ＡＢをいくつかに分け，それらを直径とする円を描く。点ＡＢのコースをいくつか考え，道のりを比べよう。」
問題を作るのは難しいが楽しかった ５９    やってよかった １７
問題を作ることは難しかった １６ みんなの意見が聞けてグループ学習が楽しかった １４
なんとかできた ７ 自分のレベルにあわせて取り組むことができた ６
一般化の考え方に感激した ５ 自分でも問題がちゃんとつくれた ５
すべての答が同じだったので不思議だった ４ 直径を分けた円の道のりが分からなかった ３
円周の公式が分かった ３ じっくり考えることができた ２
もっと時間があれば良かった ２ 円を上手にかけなかった ２
πを使うのが分かった １ 見方を変えるといろいろなことがうかんでくる １
簡単だった １ すごく頭に入った １
普通の授業と同じだった １ なるほどと思った １

２．授業の実際
（１） 　授業に当たって
ア 　課題を含む場面の設定
　数と式，数量関係の領域の学習は，他の領域の学習に比べ，系統性・累積性が強い。そこで，これらの領域の課題学習を単元末に位置付けてみた。資料５の結果から，単元の学習内容を加味した課題学習の実践を通して，自ら見いだした課題を創造的に解決していこうとする態度を身に付けるとともに，意欲的・探求的な学習の姿勢の確立や数学的な見方や考え方及びそのよさを感得できるようになると考えた。
　「１次関数」は，生徒にとって苦手意識が強い単元である。したがって，生徒が「１次関数」の課題学習に取り組むに当たって，指導上十分に考慮しておかなければならないことは，学ぶことの楽しさや，解決したときの成就感や満足感を味わうことができる課題を含む場面を設定することであると考える。そのため，次のような要件を考え，課題を含む場面を設定した。（「指導計画の作成と学習指導の工夫」平成３年５月文部省　参照）

○ 　一人一人の生徒が様々な思考や創意工夫をすることができ，意欲的な追究ができること。
… 　図形の性質を計算で考察できる。
○ 　一人一人の生徒が何らかの方法で結果を見通すことができ，一応の解決が可能であること。
… 　既習の学習内容（式，グラフについて）が生かせる。
○ 　課題を解決していく過程で，式についての数学的な見方や考え方が発揮され，そのよさが体験できること。
… 　式の傾き，切片の数値の意味を理解，活用できる。
○ 　課題を解決することによって，さらに新しい課題を見いだすことができるような発展性があること。
… 　直線の移動によって変化するものが見いだせる。
イ 　指導に当たって
　単元の学習を見通し，生徒の知的好奇心をゆさぶりながら，数学的な見方や考え方を重視した授業の展開が課題学習を成立させ，豊かな感性，自ら学ぶ意欲や態度を育成すると考えた。課題を見いだすこと，課題を解決することに十分時間を取りたいと考え，課題を見いだし，追究するまでの１時間，課題の解決・まとめで１時間，計２時間の課題学習の時間を設定し，次の３点を心掛けて授業を展開した。
（ア） 　課題を見いだす方法
　座標平面に直交している２直線を含む三つの直線を示す。その直線によって描かれた図から課題を見いだす活動をもつことによって課題を発見する手だてとしたい。「直角三角形」や「台形」に目を向けた生徒がいれば，「本当にそんな図形だろうか」，座標や線分に目を向けた生徒がいれば，「求められるかな」といった発問をし，「なぜだろう」，「本当かな」，そして「やれそうだ」と解決の見通しをもたせ，生徒に知的好奇心，自己効力感がもてるようにしたい。
　また，見いだした課題の発表の場をもち，課題発見の喜び，友達の課題を生かした新たな課題の発見への意欲を高めたい。
（イ） 　課題を含む場面を発展的に見たり考えたりする方法
　一つの直線を座標平面上で移動させ，伴って変わる図形や線分を考える場をもつことによって，直線の式の切片を変えてみるなどして，課題を見いだす視点を広げたい。第２学年での課題を含む場面の見方，課題の見いだし方が，第３学年の課題学習への取り組みにつながると考える。
（ウ） 　課題を解決する方法
　図形の面積，線分の長さ，座標を求める…といった課題を生徒たちは見いだすのではないかと考える。三角形の面積を求めるために，どこを底辺と見て，どこを高さと見るのか，課題解決のための視点を支援したり，求積しようとしている生徒を個別に集め，解決方法を援助したりしていきたいと考える。また，求められた三角形の面積を合成あるいは分解して，別な三角形や四角形の面積を求める柔軟な図形の見方も養いたいと考える。
（２） 　授業の展開
ア 　目　標 　課題を含む場面（３直線が描かれた座標平面）から課題を見いだし，切片や傾きの数値，式についての考えを生かしながら，課題を追究，解決することができる。
イ 　展開
展開
      
ウ 　授業の記録
抽出児Ａ 　筋道を立てて考えることができ，表現力や数学的技能も高い。
抽出児Ｂ 　基礎的・基本的学習内容が身に付いている。柔軟性を育てたい。
抽出児Ｃ 　基礎的・基本的学習内容の定着が十分ではないが，数学に関心をもっている。
授業の記録
記号１ … 　問題解決の楽しさや，よさ，おもしろさが感じられたと思われる生徒の様子
記号１ … 　数学的な見方や考え方が発揮されたと思われる生徒の様子

資料ａ
資料ｂ 資料ｃ
（３） 授業の分析と考察
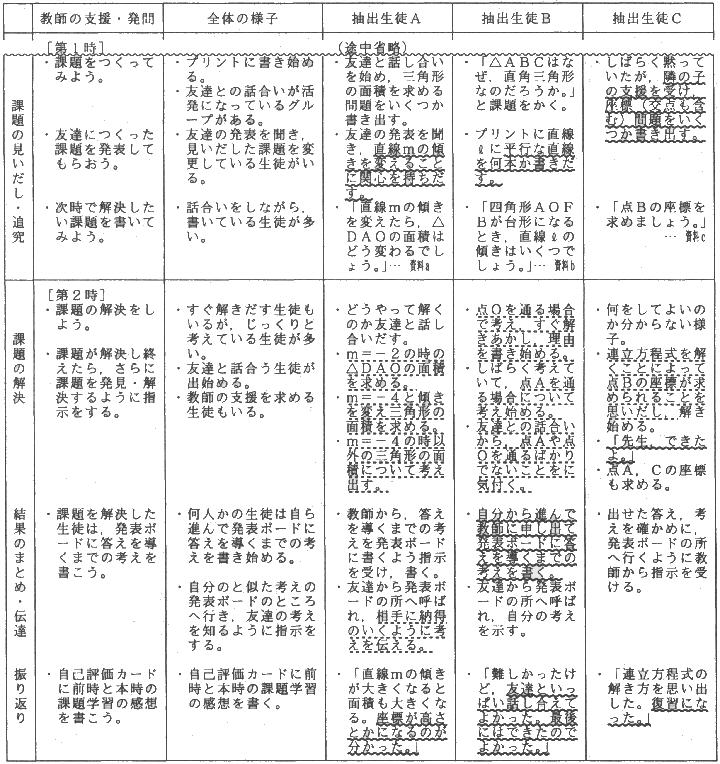
ア 　課題を見いだす活動
　課題を見いだす手だてとして二つの手だてを講じてみた。一つ目は，３直線の描かれた座標平面を提示し，「この中には，どんな図形があるのか。」と発問した。直線や座標軸によってつくられる図形に着眼し，「三角形の面積を求めましょう。」の課題を多くの生徒が見いだした。しかし，その発問をしたために，予想していた線分の長さを求めることを課題として取り組んだ生徒は一人もいなかった。「本当に直角三角形だろうか，台形だろうかなぜだろう」と問い掛け，課題を見いだす知 的好奇心を引き出すことをねらったわけだが，表現力や数学的技能の高い生徒は，直角三角形や台形など特殊な図形にかかわる課題を見いだす傾向があった。
　二つ目として，座標平面上で直線ｍの切片を固定し，あるいは傾きを固定しグラフを移動させた。座標平面上に何本もの平行線を引いたり，ｙ軸上の１点を通る直線を何本か引いたりして，課題解決の見通しを立て，課題を見いだした生徒がいた。課題を見いだせなかった生徒も，友達の課題の発表後，自分で解決できそうな課題を見いだすことができてきた。

資料６　最初に取り組んだ課題
平成９年１０月２２日実施　２年８組３９人（単位　人）
・ 　三角形の面積を求めましょう。 １３
・ 　座標を求めましょう。 ９
・ 　四角形ＡＯＦＢが台形になるとき，直線ｌの傾きはいくつでしょう。 ６
・ 　△ＡＢＣは，なぜ直角三角形といえるのでしょう。 ３
・ 　直線ｍの傾きを変えたら，三角形ＡＢＣの面積はどう変わるでしょう。 ３
・ 　四角形の面積を求めましょう。 １
・ 　△ＡＯＥが正三角形になるとき，直線ｌの傾きはいくつでしょう。 １
・ 　四角形ＡＯＦＢの二倍の面積の台形をつくるにはどの直線をどのように動かせばよいでしょう。 １
・ 　三角形ＡＯＥが二等辺三角形になるとき，直線ｌの傾きはいくつでしょう。 １
・ 　交点はいくつあるでしょう。 １
イ 　課題を解決する活動
  • 　同じような課題をつくった生徒で同一グループをつくり，話合いながら課題解決をした。
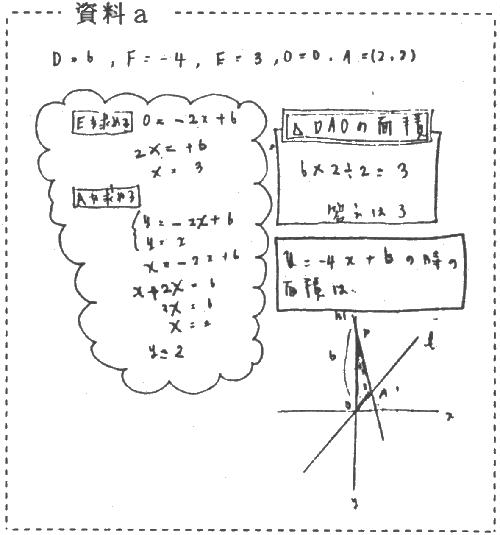
  • 　三角形の面積を求めるために，どこを底辺・高さとして考えればよいのか，またそれらの長さをどのようにして求めたらよいのか悩んでいる生徒が何人かいた。しかし，同一グループ内の課題解決の見通しをもてた生徒や教師の支援によって，課題解決をしていた。
  • 　∠ＡＢＣが直角になる理由を考えていた生徒は，分度器で角を測り課題解決としていたので，ます目の入った座標平面用紙を配付した。グループ内の話合いや教師の支援によって，合同な三角形から直角の理由を導きだした。
  • 　２時間扱いにし，課題を解決するための時間を十分に確保したので，ほとんどの生徒が課題に粘り強く取り組み解決できた。
ウ 　まとめたり，友達へ伝達したりする活動
　課題解決のまとめの時や発表ボードを使った友達への課題解決の伝達のときに，生徒の意欲的・探求的な学習の姿勢が見られ，数多くのつぶやきを聞くことができた。
  • 　「どうやればいいんだ…。」
  • 　「まず交点（の座標）をださないと…。」
  • 　「とりあえず交点（の座標）をださないと…。」
  • 　「座標はでたけど，どうすればいいのかな」
  • 　「わかんなくなっちゃった。」（発表ボードにまとめながら）
  • 　「どうやったの。」（発表ボードにまとめられた友達の考えをみて）
  • 　「これおかしいよ。」（発表ボードにまとめられた友達の考えをみて）
　自分で見いだした課題であるという自信，自分であるいは友達と解決した自信がこれらのつぶやきになったのではないかと考える。解決していく上での学習の楽しさ，そして解決したときの成就感や満足感を生徒たちは味わうことができたようだ。
　発表ボードにまとめられた友達の考えを，その友達と考える「まとめ，友達への伝達」の表現活動の時間を設けたが，一部の生徒の活動の場になってしまった点が，残念である。
エ 　自己評価カードに書かれた感想
　生徒は，自分なりのいろいろな課題を見いだし，解決できなかった課題もあったが，「いろいろな課題をつくることができた。」，「いろいろな図形について考えることができた。」，「難しい課題をつくってしまったが，いろいろと考えることができた。」といった感想から，知的好奇心や自己効力感がもてたと考えられる。
　また，交点（座標）について感想を書いている生徒も多く，既習の学習内容を活用した主体的な学習ができたと考えられる。

資料７　自己評価カードに書かれた感想
平成９年１０月２２日実施　２年８組３９人（単位　人）
　交点を求めれば面積が求められる。 ８
　いろいろな課題をつくることができた。 ７
　交点を求めれば高さなどがでる。 ６
　式の意味が分かればできる。 ２
　楽しかった。分かるようになってうれしかった。 ２
　班の人と話合ったり，意見を出しあったりして楽しく活動できた。 ２
　いろいろな図形について考えることができた。 ２
　三角形の面積を求めるだけでもいろいろな計算をしなければならない。 ２
　難しかった。 ２
　座標を求めることができた。 １
　グラフの三角形の面積が求めることができた。 １
　難しい課題をつくってしまったが，いろいろと考えることができた。 １
　連立方程式の解き方が分かった。 １
３．まとめと今後の課題
（１） 　研究のまとめ
　課題学習「１次関数」において，生徒の課題に対する関心・意欲を高めたり，生徒の気付きを生かしたりしながら，問題を解く楽しさや分かる喜びを感じ，数学的な見方や考え方を身に付けられるように授業研究に取り組んだ結果，次のようなことが明らかになった。
ア 　課題を含む問題提示場面において，問題を把握するために十分に時間をとり，課題把握をするための手だての工夫をした結果，生徒は課題を見いだす楽しさ，できそうだという自己効力感をもつことができた。
イ 　課題学習に取り組むことで，生徒は自分なりに課題を見いだすことができたという自信や自分で，あるいは友達と解決できたという成就感や満足感を味わうことができた。
ウ 　課題解決してきた過程をまとめ，友達に伝える表現活動をすることで，生徒は数学的な見方や考え方を確認したり，見方や考え方のよさを感じたりすることができた。また，多くの生徒は積極的に意見交換し，意欲的・探求的な学習の姿勢が見られるようになった。
（２） 今後の課題
　課題学習では，特に，一人一人の生徒が多くの課題を見いだし，解決方法も多様で個に応じた指導が必要であると強く感じた。そこで，ＴＴなど協力的な指導を展開し，ＴＴの特性をいろいろな学習場面において活用する研究をしていきたい。

算数・数学科目次