【授業研究１】小学校第５学年「三角形と四角形の面積」

（１）

授業に当たって ア 　児童の実態 　前提テストで，小学校４年生までの学習内容の定着度をみた。その結果，ほとんどの児童が，面積は敷き詰められた単位となる正方形の個数で表すことができることを理解しており，方眼を利用していろいろな図形の面積を求めることができていた。また，長方形の面積を，（たて）×（横）の計算で求めることも大部分の児童ができていた。中には，長方形の求積公式を忘れてしまっていたり，面積と体積の単位の表し方を混同しがちであったりする児童もやや見受けられた。なお，第４学年における面積の学習の中で，三角形などの図形についても，長方形のときと同じように求積公式があるのではないかといったところに興味が向いている児童も見られた。 　算数の学習における児童の取り組みの様子については，多くの児童が，解決の仕方をじっくりと考えたり友達と比べ合ったりする活動に進んで取り組んできた。しかし，一方では，どういう手順でやればよいかの指示を待っているような児童もおり，算数の学習に積極的に取り組もうとする児童は決して多いとは言えない。 イ 　指導に当たって 　本単元では，基本的な図形の求積方法を考える楽しさを味わいながら，既習の図形に帰着させて求積の方法を考えることができるようにしたいと考えた。そのために，ただ単に求積公式を知って活用するだけではなく，児童自ら様々な自分なりの求積方法を考え，それらをもとに公式を生み出す過程を重視することにした。 　そこで，次のようなことに焦点を当てて実践に取り組んだ。 （ア） 　単元の学習全体を見通す活動 　本単元の第１〜２時において，正方形や長方形以外の図形の面積に目を向け学習計画を立てる活動を取り入れることにした。また，その中で，基本的な図形（三角形，平行四辺形，台形）の面積については，どの図形からどのような順序で調べていくのかを，自らが決定し計画を立て，第３〜５時において求積方法を考えることにした。これは，単元全体の見通しをもち，自分の思いを生かしながら学習計画を立てることで，主体的な学習活動を促すことができると考えたからである。 資料１　学習計画表 （イ） 　自分なりの追究を促すための支援 　児童が自分なりの感じ方や考えに基づいて個性を発揮しながら解決を進めていくことができるように，同じ学習の流れを組んだ者同士で小集団をつくり，追究活動を行えるようにした。 　また，多様な学習の流れに対応してより細やかな支援ができるように，１クラス２人のＴＴで授業を組み立てることにした。その他，主体的な自力解決ができるように，ヒントコーナーを充実させ，必要に応じて児童が方眼入りの図形，透明な方眼シートなどを自由に使えるようにしてみた。このような手だてを講じることで，自分なりの追究を促すことができると考えた。 （ウ） 　小集団による話合い活動 　自分の考えを発表したり友達の考えに対する疑問や意見を自由に投げ掛け合い，お互いの考えのよさを共感し合える場として，小集団による話合い活動を取り入れることにした。小集団による活動とすることで，自分の考えが友達の考えと同等に話合いの舞台にのり，集団の中で自分を表現したり集団から自分が認められたりする機会が増える。そして，この児童同士のかかわりを通して，見方や考え方を問い直したりよさを感じたりすることができると考えた。なお，第３〜５時においては児童の活動が異なってくることから，小集団は，活動の流れが同じである４〜６名の児童で構成することにした。これにより，既習内容が同じ児童同士での話合いができるようにした。

（２）

学習指導案 ア 　学習計画　（１２時間取扱い　ー　本時は第４時） イ 　授業の展開 （ア） 　目　標 　三角形・平行四辺形・台形について，既習の面積の求め方と関連付けて自分なりの面積の求め方を考えることができる。 （イ） 展　開 　学習活動 　　支援及び留意点 　　評価

（４）

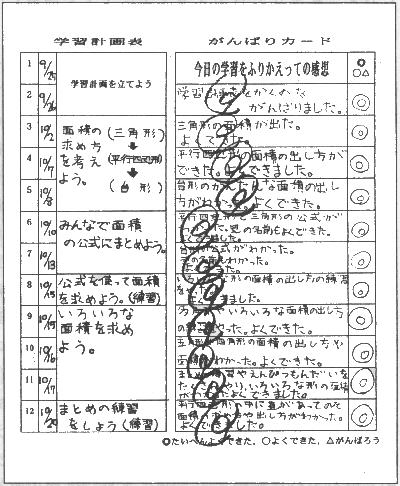
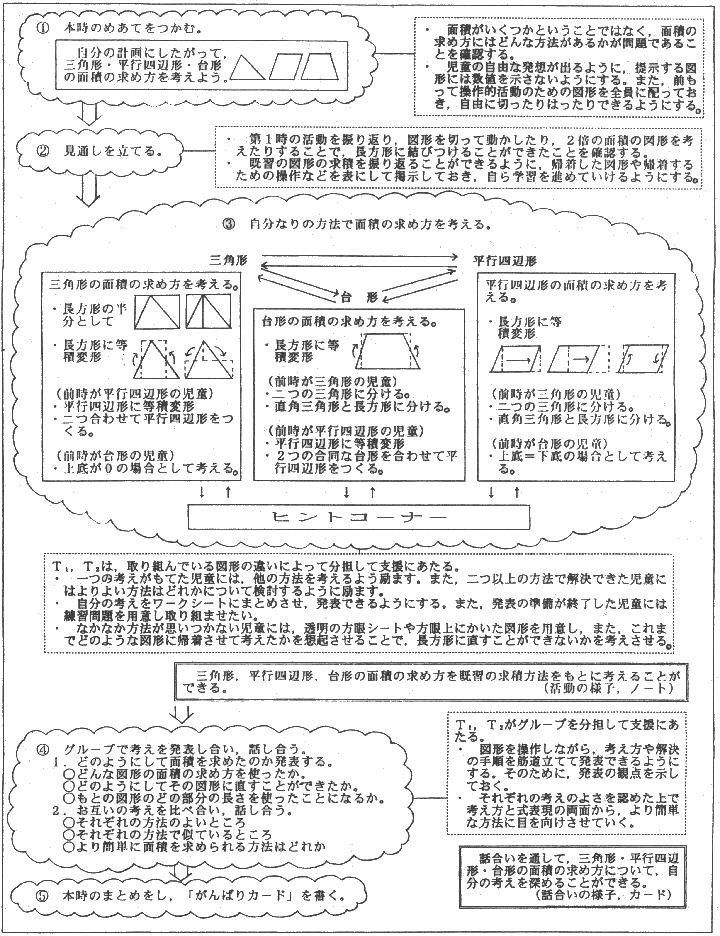
授業の分析と考察 ア 　自力解決における児童の反応と考察 　自力解決の場面において，ほとんどの児童は，見通しをもち自分なりの面積の求め方を考え出すことができた。解決の順序を決定する際に自分なりの根拠を明確にしたことが，見通しをもった自力解決につながったと思われる。また，別の考えではできないだろうかと意欲的に取り組む姿が多く見られた。つまずきがちな児童も数人いたが，ワークシート上に透明な方眼シートを重ねたり，ます目入りのワークシートを利用したりすることで，自力で考えを進めることができた。ヒントカードは５種類ほど用意してあったが，利用した児童は数人であり，その多くは二つ目や三つ目の求め方を考える際に利用していたようである。 　次に，児童の思考の面に目を向けてみると，「前の時間と同じ考え方でできないかな。」と考える児童と「前の時間に考えた形になおすことはできないかな。」と考える児童との大きく二つのタイプがあった。このように考え方に違いはあったが，既習の内容を生かそうという態度はよく表れていた。しかし，平行四辺形の面積を求めるに当たり「前の時間にやった台形の面積の求め方を使えないかな。」と考えた児童は，解決の仕方が思い付かずに，長方形への等積変形で面積を求めようと考えを変えていった。台形を最初に選んだ児童への支援という点で，もう少し工夫が必要であったと反省している。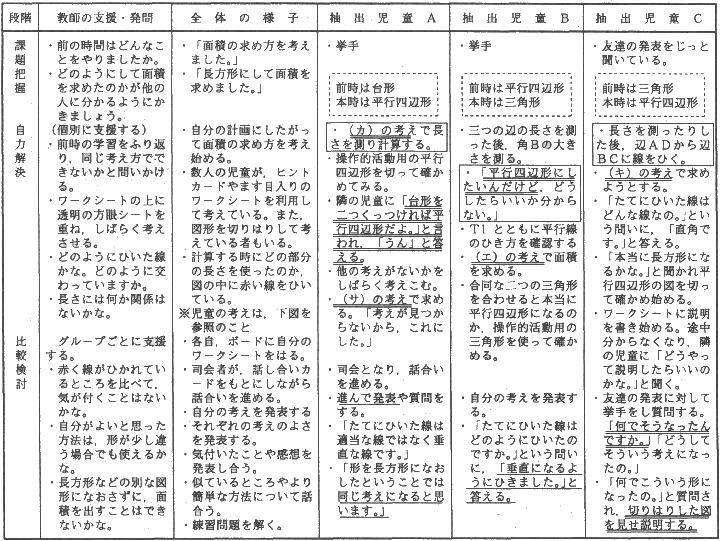 資料２　学習のてびき（順序決定・理由） イ 　小集団での話合いにおける児童の反応と考察 　小集団にすることにより，全体の場よりも自由に話ができ，進んで質問や意見のやりとりができた。抽出児童Ｃは，授業中ほとんど発言することはないが，本時においては進んで話合いに取り組めた。これは，自分なりの考えがもてたことと小集団のために自分の思いを表現しやすかったことによるのではないかと思われる。 　意見のやりとりでは，「たてに引いた線はどんな線ですか。」と質問され，直観的に引いていた高さの線を「自分は垂直な線を引きたかったんだ。」と振り返ってみることができた児童もいた。また，「やり方は違うけど，面積が同じ長方形をつくったということでは同じ考えだ。」など統合的に見ることのできた児童もいた。なお，自力解決時に長さを使った部分には赤い線を引かせておいたことから，話合いの中で，「ＢＣの長さとＡから垂直に引いた線の長さをかければ平行四辺形の面積が出る。」といったような面積の計算の仕方に気付いたグループや練習問題をやっていく中で「いちいち形をなおさなくてもできそうだぞ。」と計算の仕方に気付いたグループが出るなど，児童は自分たちなりに一般化を図ることができたと考える。しかし，台形については，自力で一般化を図ることは難しく，かなりＴ１，Ｔ２の支援が必要であった。 　小集団での比較検討の場面を振り返ってみて，だれもが自分なりの考えをもち，自分の考えが前面に出た話合い活動ができたことで，自分の考えと照らし合わせながら他の考えのよさにも目を向けることができたように思われる。なお，多様な考えを基に練り上げていく場面では，ＴＴで支援に当たったが，教師が他のグループの支援をしている時でも深まりのある話合いが進められるように，話合い用のヒントカードが必要であったと思われる。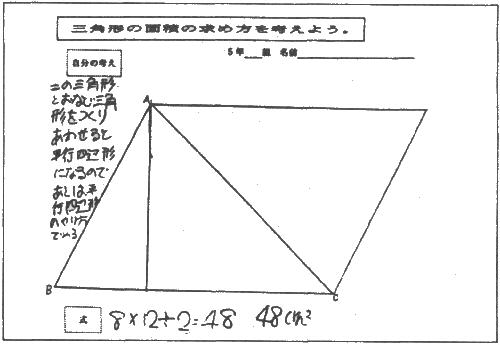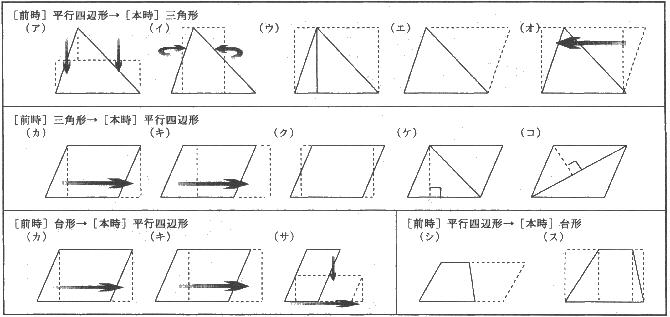 資料３　ワークシート（三角形） ウ 　抽出児の変容 　抽出児Ａは，（カ）と（サ）の二つの考えで解決したことで考える楽しさを味わうことができたと思われる。なお，最終的には，（サ）の考えで取り組み，前時に使った方法で等積変形をしていた。 　抽出児Ｂは，前時に取り組んだ図形である「平行四辺形」にしたいという思いをもち，変形しようとしていた。前時に学習した図形に帰着させようとする態度が表れていたと思われる。また，操作的活動を通して，合同な三角形を二つつなげると平行四辺形になることが確認できた。 　抽出児Ｃは，前時に三角形の求積方法を考える際に使った「たての線」のイメージを生かして（キ）の考えでスムーズに長方形に変形することができた。前時で，長方形に等積変形した際に用いたアイデアを利用しようとしていたと思われる。 エ 　算数科の学習に関するアンケートの分析と考察 　算数の学習について５段階で回答させたところ，右のような結果となった。児童が，自分なりの考えで解決を図り，更には自分の考えを深めたり生かしたりしていこうという意識で学習に取り組むことができるようになってきたと思われる。 資料４　アンケートの結果 （数値は，５段階で評価したものの平均値） （事前） 平成９年 ９月24日実施 ５年４組　31人 （事後） 平成９年 10月17日実施 ５年４組　31人 項　目 事　前 事　後 見通しをもつことができた。 ３.３ ４.０ 自分なりの考えで解くことができた。 ３.３ ４.２ 考えをよりよいものにしていこうと努力した。 ３.０ ３.７ 学習したことを次の学習に生かそうとした。 ３.６ ４.２ 数，量や図形には，喜びや楽しさがあると感じる。 ３.５ ４.０