�W　「円運動と万有引力」（高等学校第２学年）

１　単元の目標

２　単元について

　　生徒は中学校理科第1分野「運動とエネルギー」で，力の働き，物体の運動，仕事とエネルギーについて学習している。具体的には，力の働きについては，力のつり合い，合成・分解，水中で働く浮力等，物体の運動については，等速直線運動，落下運動等，仕事とエネルギーについては，仕事や仕事率，力学的エネルギー等である。また，自然界にみられる様々な事物・現象について観察，実験を行い，科学的に探究させることを通して，基本的な科学概念を中心とした知識体系を形成すること及び自然を調べる能力や態度の育成を図るとしている。
高等学校では中学校の基礎の上に，更に進んだ物理学的な方法で自然の事物・現象に関する問題を取り扱い，基本的な概念や原理・法則を理解させるとともに，探究の過程を通して，科学の方法を習得させ，科学的な自然観を育てることをねらいとしている。
　この単元では，力と運動についての基本概念や原理・法則の学習の上に立って，日常よく観察される円運動や単振動の諸性質や運動を数量的に表す方法を学習する。ここでは，複雑な数量的処理が要求され，取り扱いに苦慮するところであるが，生徒に馴染みの深い日常生活での諸場面を題材として取り上げ，生徒が興味・関心を持って学習活動に取り組むよう配慮する。向心加速度と角速度の関係については，数式的な扱いだけでなく，観察，実験を通してそれらの量的関係を実感させたい。
　万有引力についてはケプラーの法則，万有引力の法則を扱い，惑星の運動と重力による物体の運動は，いずれも万有引力を受けたときの物体の運動として，統一的に説明されることを扱う。惑星の運動については，直接静止系に立って観測できないので，天体模型，作図，コンピュータシミュレーション等を使って，直感的理解が容易になるよう配慮する。
　また，微視的世界と巨視的世界に共通して存在する円運動の不思議さや，宇宙の天体現象の雄大さに目を向けられるように学習活動を工夫するとともに，自然現象の中に規則性や法則性を発見することの素晴らしさを実感したり，問題解決の喜びを味わえるように支援したい。

３　指導計画（１１時間扱い）

４　授業の実際（第一次）＜３／４時＞

（１）	目標 　等速円運動について，仮説の設定や推論する活動を通して，角速度，周期，回転数などの基本的な物理量を理解するとともに，等速円運動の速度，加速度とそれらの量の間の関係を探究する活動に興味・関心を持って意欲的に取り組むようにする。
（２）	情報活用能力と評価 　ここでは，回転台にのせた振り子の傾きと回転台の回転数をコンピュータで計測できるようにし，振り子の傾きから計算したおもりの加速度と回転数の関係をグラフ化して，円運動の加速度と回転数あるいは角速度との関係を探究する学習活動を行う。 　円運動は，これまでに学習した物体の運動と違って，物体にかかる力の向きが絶えず変化する運動である。作図によって力や加速度を導出するという方法がよく取られるが，その際微小時間での変化量を考慮する必要が出てくる。このことが，生徒に「円運動は難しい」と感じさせる原因の一つとなっている。 　生徒が円運動に興味・関心を持ち，意欲的に学習活動を進めることは，引き続く「単振動」や「万有引力」の学習に進む前段階のステップとして，重要な意味を持つ。しかし，これまでは，生徒が難しいという印象を持ったまま学習を進めてきたというのが実状である。 　円運動の加速度と回転数の関係を探究する過程で，仮説の設定や検証にコンピュータによる実験計測を活用すると，短時間に精度のよい結果が得られ，加速度と回転数の関係をよりよく理解する上で効果がある。また，コンピュータ計測という最先端の手法で実験を行うことで，生徒が興味・関心を持ち，意欲的に取り組むものと期待できる。 　実験の手順は次のとおりである。自転車の前輪を利用した回転台を用い，回転数を計測するセンサ1と回転台上の振り子の傾きを計測するセンサ2を配置する。回転数計は，回転台に光を反射する部分と無反射の部分を交互に50組つけた円盤を取り付けたもので，その円盤に光が反射する単位時間あたりの回数に比例した電圧が出力されるようになっている。また，傾き計は，傾きによって光が通過できる面積が変わる構造を持った振り子に，LEDの光を当てその透過量で傾きを知るしくみになっている。その二つのアナログ信号を実験計測器に接続しデジタル信号に変換しコンピュータに転送する。 　コンピュータ画面には，回転数と振り子の傾き角との時間経過の様子を示し，次に，振り子の傾さ角から円運動の加速度を計算させ，加速度と回転数の関係をグラフに表示する。 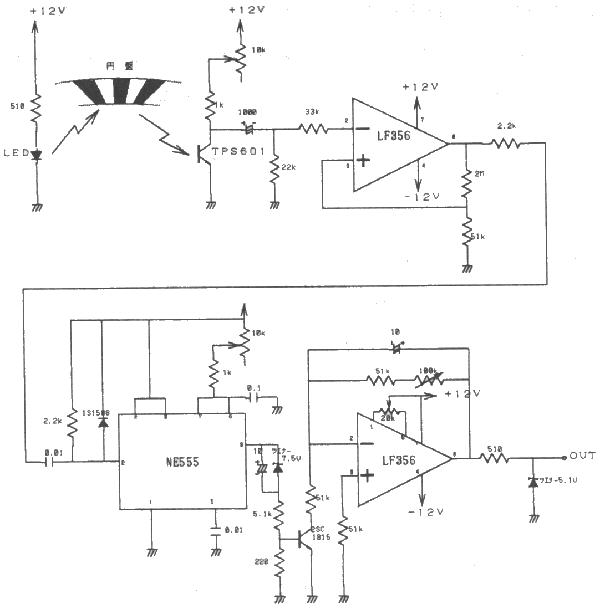図５　回転数計の回路図 図６　傾き計の回路図 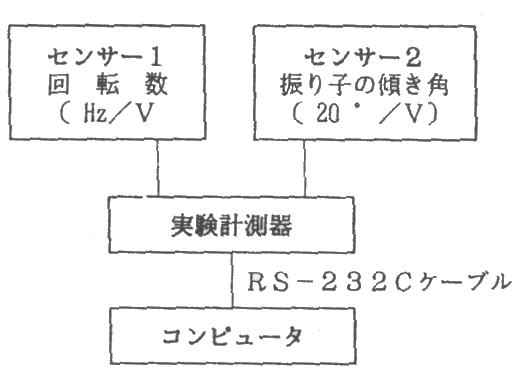図７　実験装置の概要 写真１５　装置の全景 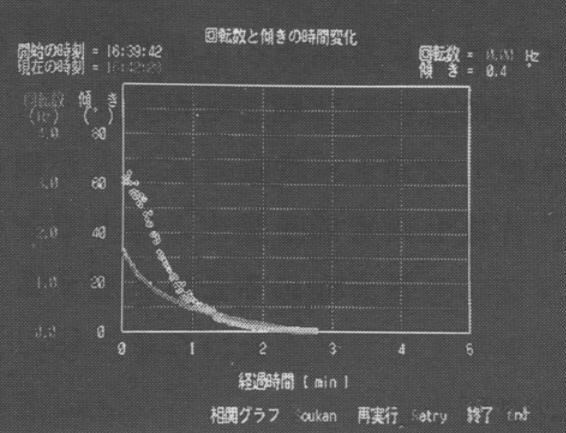写真１６　回転数と傾きの関係 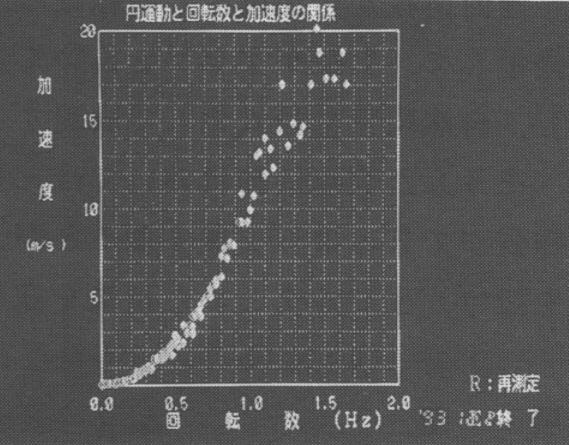写真１７　等速円運動の加速度と回転数の関係 ア 情報の判断、選択と評価 　理論的に円運動の加速度を求めるには，微小時間内での速度の変化量を作図によって求め，これから単位時間当たりの変化量を計算するという方法が一般的である。この方法では，幾何の知識を使ったり複雑な計算を経て，ようやく加速度と回転数の関係が導出できる。このような長い論理的な筋道をたどって結論に達するプロセスは，かなり高度な思考活動である。複雑な計算をせずに，加速度と回転数の関係を知る方法があれば，円運動に対する興味・関心を持続させて学習活動を進められる。 　ここでは，円運動を実際に観察しながら，加速度と回転数の関係をグラフから視覚的に把握できる方法を取り上げた。この学習活動では，現実に目の前で起こっている物理現象とそこに現れている規則性を関連させて，現象の根底にある法則性に気付きやすいという利点がある。一方，コンピュータ，回転装置，光センサなどを使い，実験装置としてはかなり大がかりなものになるので，どこからの情報がポイントになるかを選択したり，コンピュータに表示されたデータが妥当であるか，立てた仮説の検証に有用であるかなどを判断したりする活動を支援する。その際，生徒の選択や判断の根拠や背景をとらえて認めるように努める。 イ 情報の整理，処理と評価 　加速度と回転数を測定する実験は，教卓での教師による演示という形態になるが，生徒が主体的に実験に取り組むという視点に立って，既知の情報からおもりに働いている力を見いだす活動を支援する必要がある。その際，向心力と遠心力の違いに目を向けさせ，力のつり合いを利用して向心力を計算させる場面をとらえて，既習の知識を使って問題解決する様子を観察して個性の把握に努め，意欲を読み取るようにする。 　作図によって加速度を求める方法では演繹的な推論が主な思考活動になるが，実験結果から加速度と回転数の関係を求めるには，それらの量をグラフにするなどして帰納的に量的関係を数式化することになる。演繹的な導出法に慣れている生徒は，帰納的推論に心理的抵抗を示すかも知れないが，生徒のつぶやきなどから生徒の推論過程を察知するようにする。 ウ 情報の創造，伝達と評価 　生徒の意欲や個性は，表現活動を通してよりはっきりととらえることができる。また，自然の事象から得た物体の運動についての見方や考え方の広がりや深まりも表現活動から併せてとらえることができる。 　画面情報から加速度と回転数の関係を類推させる活動において，実験データを数値のまま提示して，生徒がグラフを描いて量的関係を数式化することに意欲的に取り組むように支援し，自然現象を数式化して表現するという物理学の本源的営みを体験させたい。 　そうした表現活動においては，生徒の個性に十分配慮しながら，生徒一人一人が創意ある報告ができるよう支援することが大切である。また，作成したものを発表し合うなどの機会を設け，生徒がまとめた結果を認めることによって生徒の意欲を高めるよう配慮する。
（３）	展　　開
（４）	生徒の反応 ア 　アンケートに見る生徒の反応 アンケート調査では 　わかりやすかった。 　どんなことが起こるか楽しみだった。 　またコンピュータを使って学習したい。 　実験方法が理解できた。 　実験から法則が理解できた。 　コンピュータが法則の理解に役に立った。 といった項目に肯定的に答える生徒が多かった。このことからも，学習活動が生徒にとって興味深いものだったことがうかがわれる。 イ 　感想文に見る生徒の反応 次に実験の感想の中の主なものを示す。 　自分達でコンピュータの操作ができたら，もっと楽しかったと思う。 　実際に目で見ることのできないことを，コンピュータで観察できとても参考になった。 こういう機会がもっと欲しい。 　コンピュータによる実験によって，円運動がすこしわかったように思う。特に，回転台を回したとき，すぐ画面に結果が描かれるのがとても興味深かった。今度は自分で実験装置を操作したい。 　コンピュータを使っての実験は初めてであったが，正確な結果に感動した。また，科学の進歩にも驚いた。 　円運動の加速度が回転数の2乗に比例するということが，実験からあのようにきれいに 出てきたことには驚いた。
（５）	考察 　授業前の「円運動の加速度を測定するにはどうしたらよいか。」という質問に対して，具体的な方法を答えたのは生徒の約3割であった。直線運動の加速度の学習のときに行った同様の調査では8割以上の生徒が具体的な方法を答えており，「j運動では直線運動に比べて格段に低い回答率となっている。これは，繰り返し運動として日常的によく見ているはずの円運動ではあっても，これを運動学的視点から具体的にイメージ化することが非常に難しいことを示している。 　生徒の感想にあるように，コンピュータを活用した実験計測を行ったことで，よく見慣れている円運動を観察，実験の対象として再認識させることができた。生徒の反応は予想以上に良く，もっとコンピュータを使って学習したいと答えた生徒が多く，コンピュータによる実験計測は生徒に大きなインパクトを与えた。
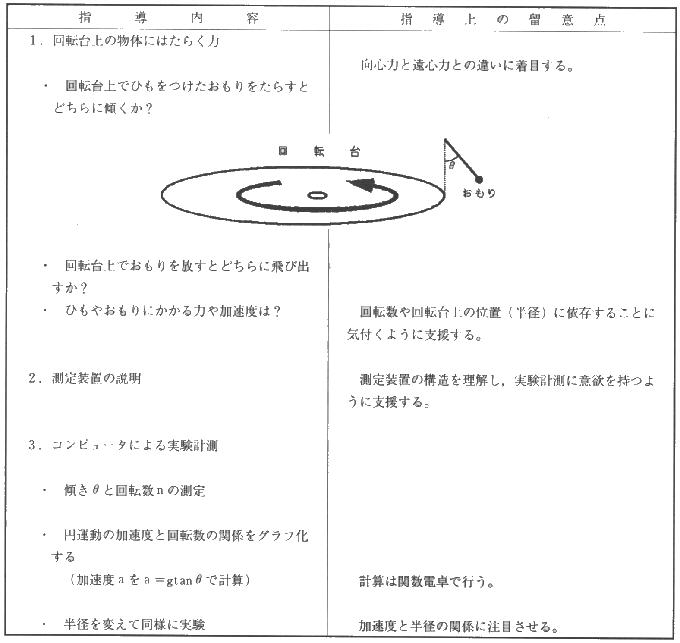
（６）	情報活用能力の評価の実際 　「回転台上でひもをつけたおもりをたらすとどちらに傾くか。」という発問には，回転台を現実に目の前に見ているということもあり，すぐに「外側に傾く。」と判断できた。実際に具体的な回転装置を見ることで，興味・関心を持たせるとともに，運動の様子を想像することが容易となり，その後の学習への意欲を持つことができた。 　振り子の傾きに関連する物理量を選択する場面では，「回転数に依存しそうだ。」という意見が多くの生徒から出され，回転数と振り子の傾きの間には何らかの関連性があるということに生徒はすぐに気付くことができた。 　向心力と遠心力の違いを考察する段階では，多くの生徒に混乱が見られた。このことは常に見受けられることであるが，実際に回転台上の振り子の運動を観察して，生徒はそれらが立場による見え方の違いであることを実感した。 　加速度と回転数の関係をグラフ化する活動では，傾きの角度から加速度を計算し，回転台の回転数の測定値と合わせてグラフにし，加速度と回転数の関数関係を予想した。生徒は回転数と傾きの測定が終わると同時にグラフ化に取り組み，法則性を見いだすことに意欲的であった。また，グラフから加速度が回転数の2乗に比例すると予想した後，コンピュータ実験計測の結果がディスプレイ画面上に表示された瞬間に「おぉ！」という歓声が上がった。こうした反応から，円運動の不思議さと自然現象の法則性が生徒の心に焼き付いたという印象を受けた。